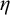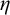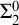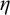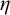1 Introduction
Coding one type of mathematical object into another is a common theme throughout mathematics. For instance, every Boolean algebra can be coded as a ring, and Fourier series are a way of coding periodic functions as vectors in
![]() $\ell _2$
. One of the simplest objects to code are sets of natural numbers. We can code subsets of
$\ell _2$
. One of the simplest objects to code are sets of natural numbers. We can code subsets of
![]() $\omega $
as real numbers using binary expansions. Subsets of
$\omega $
as real numbers using binary expansions. Subsets of
![]() $\omega $
can be coded as graphs using daisy graph: we create an isolated vertex with n many loops for each
$\omega $
can be coded as graphs using daisy graph: we create an isolated vertex with n many loops for each
![]() $n\in A$
. Using a similar idea we can code a set
$n\in A$
. Using a similar idea we can code a set
![]() $A\subseteq \omega $
as a partial order: take a chain of length n for each
$A\subseteq \omega $
as a partial order: take a chain of length n for each
![]() $n\in A$
. Encoding sets into fields is not as easy. One idea is to choose which polynomials are irreducible. This is complicated though as when adding a root to one polynomial other previously irreducible polynomials can become reducible, so a careful choice of polynomials that represent the natural numbers is needed. For linear orders, Fellner [Reference Frolov and Zubkov4] came up with the following natural way of encoding sets.
$n\in A$
. Encoding sets into fields is not as easy. One idea is to choose which polynomials are irreducible. This is complicated though as when adding a root to one polynomial other previously irreducible polynomials can become reducible, so a careful choice of polynomials that represent the natural numbers is needed. For linear orders, Fellner [Reference Frolov and Zubkov4] came up with the following natural way of encoding sets.
Definition 1.1. For a set A a linear order L is said to be an
![]() $\eta $
-representation of A if there is a surjective function
$\eta $
-representation of A if there is a surjective function
![]() $F:\omega \rightarrow A$
such that L has order type
$F:\omega \rightarrow A$
such that L has order type
where
![]() $\eta $
is the order type of
$\eta $
is the order type of
![]() $\mathbb {Q}$
. We say L is a strong
$\mathbb {Q}$
. We say L is a strong
![]() $\eta $
-representation if the function F is strictly increasing and an increasing
$\eta $
-representation if the function F is strictly increasing and an increasing
![]() $\eta $
-representation if F is non-decreasing. If a set A has a computable (strong, increasing)
$\eta $
-representation if F is non-decreasing. If a set A has a computable (strong, increasing)
![]() $\eta $
-representation then we say A is (strongly, increasingly)
$\eta $
-representation then we say A is (strongly, increasingly)
![]() $\eta $
-representable. A degree is (strongly, increasingly)
$\eta $
-representable. A degree is (strongly, increasingly)
![]() $\eta $
-representable if it contains a set that is (strongly, increasingly)
$\eta $
-representable if it contains a set that is (strongly, increasingly)
![]() $\eta $
-representable.
$\eta $
-representable.
Note that an
![]() $\eta $
-representation of A cannot tell us if
$\eta $
-representation of A cannot tell us if
![]() $0$
or 1 is in A so we will assume that
$0$
or 1 is in A so we will assume that
![]() $0,1\notin A$
when we are talking about representations of A.
$0,1\notin A$
when we are talking about representations of A.
Computability theory gives us a way of analyzing the effectiveness of such encodings and how easy it is to go from an encoding of a structure or set back to the original. For example, in the case of daisy graphs we can characterize the sets with computable daisy graph as the c.e. sets.
In this context, a natural question to ask is what sets, or degrees, have computable (strong, increasing)
![]() $\eta $
-representations. In his thesis, Fellner [Reference Frolov and Zubkov4] introduced the notion of a strong
$\eta $
-representations. In his thesis, Fellner [Reference Frolov and Zubkov4] introduced the notion of a strong
![]() $\eta $
-representation (predating the introduction of general
$\eta $
-representation (predating the introduction of general
![]() $\eta $
-representations) and proved that every set with a computable strong
$\eta $
-representations) and proved that every set with a computable strong
![]() $\eta $
-representation is
$\eta $
-representation is
![]() $\Delta ^0_3$
and that every
$\Delta ^0_3$
and that every
![]() $\Sigma ^0_2$
and every
$\Sigma ^0_2$
and every
![]() $\Pi ^0_2$
set is strongly
$\Pi ^0_2$
set is strongly
![]() $\eta $
-representable.
$\eta $
-representable.
For the case of general
![]() $\eta $
-representations we first look at the following definitions.
$\eta $
-representations we first look at the following definitions.
Definition 1.2. For any linear order L the successor relation
![]() $S_L$
on L is defined by
$S_L$
on L is defined by
![]() $S_L(x,y)\iff |[x,y]|=2$
. The block relation
$S_L(x,y)\iff |[x,y]|=2$
. The block relation
![]() $B_L$
is given by
$B_L$
is given by
![]() $B_L(x,y)\iff [x,y]\text { and } [y,x] \text { are finite}$
. A block of size n in L is a collection
$B_L(x,y)\iff [x,y]\text { and } [y,x] \text { are finite}$
. A block of size n in L is a collection
![]() $x_0<_L\dots <_L x_{n-1}$
such that
$x_0<_L\dots <_L x_{n-1}$
such that
![]() $B_L(x_0,y)\rightarrow \bigvee _{i<n} y=x_i$
.
$B_L(x_0,y)\rightarrow \bigvee _{i<n} y=x_i$
.
For any linear order L, one can see that
![]() $S_L$
is
$S_L$
is
![]() $\Pi ^0_1$
in L and
$\Pi ^0_1$
in L and
![]() $B_L$
is
$B_L$
is
![]() $\Sigma ^0_2$
in L. Feiner [Reference Fellner3] proved the following:
$\Sigma ^0_2$
in L. Feiner [Reference Fellner3] proved the following:
Theorem 1.3. For a linear order L, the set
![]() $\{n: L\text { has a block of size }n\}$
is
$\{n: L\text { has a block of size }n\}$
is
![]() $\Sigma ^0_3$
in L.
$\Sigma ^0_3$
in L.
For an
![]() $\eta $
-representation L of a set A, we have
$\eta $
-representation L of a set A, we have
![]() $A=\{n: L\text { has a block of size }n\}$
. This gives us the following.
$A=\{n: L\text { has a block of size }n\}$
. This gives us the following.
Corollary 1.4. If a set A has a computable
![]() $\eta $
-representation then A is
$\eta $
-representation then A is
![]() $\Sigma ^0_3$
.
$\Sigma ^0_3$
.
Coles et al. [Reference Coles, Downey and Khoussainov1] show the reverse of theorem 1.3 is true for general linear orders.
Theorem 1.5. For any
![]() $\Sigma ^0_3$
set A there is a computable linear order L, such that
$\Sigma ^0_3$
set A there is a computable linear order L, such that
![]() $A=\{n: L\text { has a block of size }n\}$
.
$A=\{n: L\text { has a block of size }n\}$
.
Fellner [Reference Frolov and Zubkov4] showed that every strongly
![]() $\eta $
-representable set is
$\eta $
-representable set is
![]() $\Delta ^0_3$
and went on to conjecture that every
$\Delta ^0_3$
and went on to conjecture that every
![]() $\Delta ^0_3$
set has a strong
$\Delta ^0_3$
set has a strong
![]() $\eta $
-representation. However, Lerman [Reference Lerman11] later showed that this is not the case.
$\eta $
-representation. However, Lerman [Reference Lerman11] later showed that this is not the case.
Theorem 1.6. (Lerman [Reference Lerman11])
There is a
![]() $\Delta ^0_3$
set with no computable
$\Delta ^0_3$
set with no computable
![]() $\eta $
-representation.
$\eta $
-representation.
Lerman also characterized the m-degrees with computable
![]() $\eta $
-representations showing that they are the
$\eta $
-representations showing that they are the
![]() $\Sigma ^0_3$
degrees:
$\Sigma ^0_3$
degrees:
Theorem 1.7. (Lerman [Reference Lerman11])
If A is
![]() $\Sigma ^0_3$
then
$\Sigma ^0_3$
then
![]() $A\oplus \omega $
has a computable
$A\oplus \omega $
has a computable
![]() $\eta $
-representation.
$\eta $
-representation.
This leaves open the questions of what are the (strongly)
![]() $\eta $
-representable sets and what are the strongly
$\eta $
-representable sets and what are the strongly
![]() $\eta $
-representable degrees. In the case of
$\eta $
-representable degrees. In the case of
![]() $\eta $
-representations Harris [Reference Hirschfeldt, Khoussainov and Semukhin6] came up with a characterization involving limitwise monotonic functions. Limitwise monotonic functions were first introduced by Khoussainov et al. [Reference Lerman10].
$\eta $
-representations Harris [Reference Hirschfeldt, Khoussainov and Semukhin6] came up with a characterization involving limitwise monotonic functions. Limitwise monotonic functions were first introduced by Khoussainov et al. [Reference Lerman10].
Definition 1.8. A function
![]() $F:\omega \rightarrow \omega $
is limitwise monotonic if there is a computable function
$F:\omega \rightarrow \omega $
is limitwise monotonic if there is a computable function
![]() $f:\omega ^2\rightarrow \omega $
such that
$f:\omega ^2\rightarrow \omega $
such that
![]() $F(n)=\lim _{s} f(n,s)$
and for all
$F(n)=\lim _{s} f(n,s)$
and for all
![]() $n,s$
,
$n,s$
,
![]() $f(n,s)\le f(n,s+1)$
.
$f(n,s)\le f(n,s+1)$
.
By the limit lemma, if F is limitwise monotonic then F is
![]() $\Delta ^0_2$
, and hence if
$\Delta ^0_2$
, and hence if
![]() $A=\mathrm {range}(F)$
then A is
$A=\mathrm {range}(F)$
then A is
![]() $\Sigma ^0_2$
.
$\Sigma ^0_2$
.
Limitwise monotonic functions have been used to solve questions computable model theory [Reference Kach and Turetsky7, Reference Khoussainov, Nies and Shore9, Reference Lerman10]. In particular Coles et al. [Reference Coles, Downey and Khoussainov1] proved that for any computable
![]() $\eta $
-like linear order (a class that includes computable
$\eta $
-like linear order (a class that includes computable
![]() $\eta $
-representations) that the set
$\eta $
-representations) that the set
![]() $\{n: L\text { has a block of size }n\}$
is the range of a
$\{n: L\text { has a block of size }n\}$
is the range of a
![]() $\mathbf {0}'$
-limitwise monotonic function. Harris [Reference Hirschfeldt, Khoussainov and Semukhin6] showed the reverse direction holds for computable
$\mathbf {0}'$
-limitwise monotonic function. Harris [Reference Hirschfeldt, Khoussainov and Semukhin6] showed the reverse direction holds for computable
![]() $\eta $
-representations.
$\eta $
-representations.
Theorem 1.9. A set A is
![]() $\eta $
-representable if and only if A is the range of a
$\eta $
-representable if and only if A is the range of a
![]() $\mathbf {0}'$
-limitwise monotonic function.
$\mathbf {0}'$
-limitwise monotonic function.
The construction of the
![]() $\eta $
-representation L is performed uniformly, constructing linear orders
$\eta $
-representation L is performed uniformly, constructing linear orders
![]() $L_n\cong \eta + F(n)$
and taking
$L_n\cong \eta + F(n)$
and taking
![]() $L=\sum _n L_n$
. From this it can be seen that if A is the range of a strictly increasing
$L=\sum _n L_n$
. From this it can be seen that if A is the range of a strictly increasing
![]() $\mathbf {0}'$
-limitwise monotonic function then A is strongly
$\mathbf {0}'$
-limitwise monotonic function then A is strongly
![]() $\eta $
-representable. However, Harris [Reference Hirschfeldt, Khoussainov and Semukhin6] showed that this is not a characterization of the strongly
$\eta $
-representable. However, Harris [Reference Hirschfeldt, Khoussainov and Semukhin6] showed that this is not a characterization of the strongly
![]() $\eta $
-representable sets.
$\eta $
-representable sets.
Harris also showed that the degrees with computable strong
![]() $\eta $
-representations are not trivial.
$\eta $
-representations are not trivial.
Theorem 1.10. (Harris [Reference Hirschfeldt, Khoussainov and Semukhin6])
There is a
![]() $\Delta ^0_3$
degree that does not contain a set with a computable strong
$\Delta ^0_3$
degree that does not contain a set with a computable strong
![]() $\eta $
-representation.
$\eta $
-representation.
Kach and Turetsky [Reference Kalimullin, Khoussainov and Melnikov8] modified the notion of limitwise monotonic to give the following:
Definition 1.11. A function
![]() $F:\mathbb {Q}\rightarrow \omega $
is support (strictly) increasing limitwise monotonic function on
$F:\mathbb {Q}\rightarrow \omega $
is support (strictly) increasing limitwise monotonic function on
![]() $\mathbb {Q}$
if there is computable
$\mathbb {Q}$
if there is computable
![]() $f:\mathbb {Q}\times \omega \rightarrow \omega $
such that
$f:\mathbb {Q}\times \omega \rightarrow \omega $
such that
-
•
 $F(q)=\lim _sf(q,s)$
.
$F(q)=\lim _sf(q,s)$
. -
• For all
 $q,s \ f(q,s)\le f(q,s+1)$
.
$q,s \ f(q,s)\le f(q,s+1)$
. -
• The set
 $S:=\{q\in \mathbb {Q}: F(q)\ne 0\}$
has order type
$S:=\{q\in \mathbb {Q}: F(q)\ne 0\}$
has order type
 $\omega $
.
$\omega $
. -
•
 $F\restriction S$
is (strictly) increasing.
$F\restriction S$
is (strictly) increasing.
One can relativize this to a degree
![]() $\mathbf {d}$
by allowing f to be
$\mathbf {d}$
by allowing f to be
![]() $\mathbf {d}$
-computable. They define
$\mathbf {d}$
-computable. They define
![]() $\mathbf {SILM}^{\mathbf {d}}(\mathbb {Q})$
to be the set of A such that A is the range of a
$\mathbf {SILM}^{\mathbf {d}}(\mathbb {Q})$
to be the set of A such that A is the range of a
![]() $\mathbf {d}$
-support increasing limitwise monotonic function on
$\mathbf {d}$
-support increasing limitwise monotonic function on
![]() $\mathbb {Q}$
and
$\mathbb {Q}$
and
![]() $\mathbf {SSILM}^{\mathbf {d}}(\mathbb {Q})$
to be the set of A such that A is the range of a
$\mathbf {SSILM}^{\mathbf {d}}(\mathbb {Q})$
to be the set of A such that A is the range of a
![]() $\mathbf {d}$
-support strictly increasing limitwise monotonic function on
$\mathbf {d}$
-support strictly increasing limitwise monotonic function on
![]() $\mathbb {Q}$
.
$\mathbb {Q}$
.
Kach and Turetsky were able to get the following result about increasing
![]() $\eta $
-representations.
$\eta $
-representations.
Theorem 1.12. A set A has a computable increasing
![]() $\eta $
-representation if and only if
$\eta $
-representation if and only if
![]() $A\in \mathbf {SILM}^{\mathbf {0}'}(\mathbb {Q})$
.
$A\in \mathbf {SILM}^{\mathbf {0}'}(\mathbb {Q})$
.
Similarly to the case of
![]() $\eta $
-representable degrees, Kach and Turetsky proved that every
$\eta $
-representable degrees, Kach and Turetsky proved that every
![]() $\Delta ^0_3$
degree has a computable increasing
$\Delta ^0_3$
degree has a computable increasing
![]() $\eta $
-representation (proved earlier in [Reference Harris5]).
$\eta $
-representation (proved earlier in [Reference Harris5]).
Like in the case of Theorem 1.9, the proof of Theorem 1.12 gives us that if
![]() $A\in \mathbf {SSILM}^{\mathbf {0}'}(\mathbb {Q})$
then A is strongly
$A\in \mathbf {SSILM}^{\mathbf {0}'}(\mathbb {Q})$
then A is strongly
![]() $\eta $
-representable. The converse, however, is not true in general.
$\eta $
-representable. The converse, however, is not true in general.
Theorem 1.13. (Turetsky [Reference Feiner2])
There is a set
![]() $A\notin \mathbf {SSILM}^{\mathbf {0}'}(\mathbb {Q})$
with a computable strong
$A\notin \mathbf {SSILM}^{\mathbf {0}'}(\mathbb {Q})$
with a computable strong
![]() $\eta $
-representation.
$\eta $
-representation.
This is close to a characterization of strongly
![]() $\eta $
-representable sets. In Section 4 we are able to prove that for dense enough sets this is a characterization.
$\eta $
-representable sets. In Section 4 we are able to prove that for dense enough sets this is a characterization.
Corollary 1.14. Suppose
![]() $g:\omega \rightarrow \omega $
is a
$g:\omega \rightarrow \omega $
is a
![]() $\mathbf {0}'$
-computable increasing function. If a set A has a strong
$\mathbf {0}'$
-computable increasing function. If a set A has a strong
![]() $\eta $
-representation and satisfies
$\eta $
-representation and satisfies
![]() $|A\cap g(n)|\ge n$
for all n then
$|A\cap g(n)|\ge n$
for all n then
![]() $A\in \mathbf {SSILM}^{0'}(\mathbb {Q})$
.
$A\in \mathbf {SSILM}^{0'}(\mathbb {Q})$
.
Using this we are then able to characterize the sets with computable strong
![]() $\eta $
-representations up to many-one degree.
$\eta $
-representations up to many-one degree.
Corollary 1.15. The following coincide.
-
• The m-degrees of sets with computable strong
 $\eta $
-representations.
$\eta $
-representations. -
• The m-degrees of sets in
 $\mathbf {SSILM}^{\mathbf {0}'}(\mathbb {Q})$
.
$\mathbf {SSILM}^{\mathbf {0}'}(\mathbb {Q})$
. -
• The m-degrees of sets with
 $\Delta ^0_2$
strong
$\Delta ^0_2$
strong
 $\eta $
-s-representations.
$\eta $
-s-representations.
2
 $\eta $
-s-Representations
$\eta $
-s-Representations
The existing characterizations of sets with computable
![]() $\eta $
-representations and with computable increasing
$\eta $
-representations and with computable increasing
![]() $\eta $
-representations both involve relativizing some construction to
$\eta $
-representations both involve relativizing some construction to
![]() $\mathbf {0}'$
and make use of the fact that
$\mathbf {0}'$
and make use of the fact that
![]() $\mathbf {0}'$
can compute the successor relation on any computable linear order. For this reason we propose the following definition.
$\mathbf {0}'$
can compute the successor relation on any computable linear order. For this reason we propose the following definition.
Definition 2.1. A (strong)
![]() $\eta $
-s-representation of a set A is a computable (strong)
$\eta $
-s-representation of a set A is a computable (strong)
![]() $\eta $
-representation L where the successor relation
$\eta $
-representation L where the successor relation
![]() $S_L$
is also computable.
$S_L$
is also computable.
The hope is that we can find a characterization of strongly
![]() $\eta $
-s-representable sets and turn it into a characterization of the strongly
$\eta $
-s-representable sets and turn it into a characterization of the strongly
![]() $\eta $
-representable sets. Towards this idea we have the following theorem.
$\eta $
-representable sets. Towards this idea we have the following theorem.
Theorem 2.2. If L is a
![]() $\mathbf {0}'$
-computable
$\mathbf {0}'$
-computable
![]() $\eta $
-representation of some set A and the block relation
$\eta $
-representation of some set A and the block relation
![]() $B_L\le _T \mathbf {0}'$
then there is a computable linear order D such that
$B_L\le _T \mathbf {0}'$
then there is a computable linear order D such that
![]() $D\cong L$
and
$D\cong L$
and
![]() $B_D\le _T \mathbf {0}'$
.
$B_D\le _T \mathbf {0}'$
.
Proof Using that L is
![]() $\Delta ^0_2$
we can approximate L in stages. We keep track of the blocks that
$\Delta ^0_2$
we can approximate L in stages. We keep track of the blocks that
![]() $\emptyset ^{\prime }_s$
thinks are in
$\emptyset ^{\prime }_s$
thinks are in
![]() $L_s$
and build corresponding blocks in
$L_s$
and build corresponding blocks in
![]() $D_s$
. When we see two blocks in
$D_s$
. When we see two blocks in
![]() $L_s$
change order or merge, we keep the representative of the block with the smallest member (in the sense of
$L_s$
change order or merge, we keep the representative of the block with the smallest member (in the sense of
![]() $<_{\mathbb {N}}$
) and remove the other one by densifying (i.e., adding points so that the block becomes part of a copy of
$<_{\mathbb {N}}$
) and remove the other one by densifying (i.e., adding points so that the block becomes part of a copy of
![]() $\mathbb {Q}$
). Then we add a new block in the correct place if needed.
$\mathbb {Q}$
). Then we add a new block in the correct place if needed.
More formally, let
![]() $(L_s,<_s,B_s){}_{s}$
be a sequence of linear orders with block relation that has limit
$(L_s,<_s,B_s){}_{s}$
be a sequence of linear orders with block relation that has limit
![]() $(L,<_L, B)$
where each
$(L,<_L, B)$
where each
![]() $L_s\subseteq L_{s+1}$
is a subset of
$L_s\subseteq L_{s+1}$
is a subset of
![]() $\omega $
.
$\omega $
.
Define
![]() $D_0=\emptyset $
. We will keep a follower function
$D_0=\emptyset $
. We will keep a follower function
![]() $f_s$
from the blocks of
$f_s$
from the blocks of
![]() $D_s$
to a corresponding element in
$D_s$
to a corresponding element in
![]() $L_s$
that represents the block. At stage s, for any
$L_s$
that represents the block. At stage s, for any
![]() $b_i,b_j\in \mathrm {dom}(f_s)$
if we have
$b_i,b_j\in \mathrm {dom}(f_s)$
if we have
![]() $f_s(b_i)<_{\mathbb {N}} f_s(b_j)$
and
$f_s(b_i)<_{\mathbb {N}} f_s(b_j)$
and
![]() $f_s(b_i)<_s f_s(b_j)$
but
$f_s(b_i)<_s f_s(b_j)$
but
![]() $ f_s(b_i)>_{s+1} f_s(b_j)$
then in
$ f_s(b_i)>_{s+1} f_s(b_j)$
then in
![]() $D_{s+1}$
we will remove
$D_{s+1}$
we will remove
![]() $b_j$
from
$b_j$
from
![]() $\mathrm {dom}(f_{s+1})$
. Similarly if
$\mathrm {dom}(f_{s+1})$
. Similarly if
![]() $f_s(b_i)>_s f_s(b_j)$
but
$f_s(b_i)>_s f_s(b_j)$
but
![]() $ f_s(b_i)<_{s+1} f(b_j)$
or
$ f_s(b_i)<_{s+1} f(b_j)$
or
![]() $\neg B_s(f_s(b_i), f_s(b_j))$
but
$\neg B_s(f_s(b_i), f_s(b_j))$
but
![]() $B_{s+1}(f_s(b_i), f_s(b_j))$
.
$B_{s+1}(f_s(b_i), f_s(b_j))$
.
Next, for each block
![]() $b\in \mathrm {dom}(f_s)$
that has not been removed we make sure it has the correct size. Let
$b\in \mathrm {dom}(f_s)$
that has not been removed we make sure it has the correct size. Let
![]() $y=\min _{\mathbb {N}}\{x: B_s(x,f_s(b))\land \neg B_{s+1}(x,f_{s}(b))\}$
. If y exists, remove points from the end of b so that it has size
$y=\min _{\mathbb {N}}\{x: B_s(x,f_s(b))\land \neg B_{s+1}(x,f_{s}(b))\}$
. If y exists, remove points from the end of b so that it has size
![]() $|\{x<_{\mathbb {N}} y: B_{s}(x,f_s(b))\}|$
. Now we add points to the end of the block so that the block of
$|\{x<_{\mathbb {N}} y: B_{s}(x,f_s(b))\}|$
. Now we add points to the end of the block so that the block of
![]() $f_{s}(b)$
in
$f_{s}(b)$
in
![]() $L_{s+1}$
will have the same size as b does in
$L_{s+1}$
will have the same size as b does in
![]() $D_{s+1}$
. Then, in case small numbers have been added we set
$D_{s+1}$
. Then, in case small numbers have been added we set
![]() $f_{s+1}(b)=\min _{\mathbb {N}}\{x: B_{s+1}(x,f_s(b))\}$
.
$f_{s+1}(b)=\min _{\mathbb {N}}\{x: B_{s+1}(x,f_s(b))\}$
.
Then for each block c in
![]() $L_{s+1}$
that does not have an element in
$L_{s+1}$
that does not have an element in
![]() $\mathrm {range}(f_s)$
we create a corresponding block b in
$\mathrm {range}(f_s)$
we create a corresponding block b in
![]() $D_{s+1}$
of the same size as c and set
$D_{s+1}$
of the same size as c and set
![]() $f_{s+1}(b)=\min _{\mathbb {N}}(c)$
. Finally we densify; for all adjacent
$f_{s+1}(b)=\min _{\mathbb {N}}(c)$
. Finally we densify; for all adjacent
![]() $x,y$
which are not part of the same block in
$x,y$
which are not part of the same block in
![]() $\mathrm {dom}(f_{s+1})$
, we add a new point between x and y. We now have
$\mathrm {dom}(f_{s+1})$
, we add a new point between x and y. We now have
![]() $D_{s+1}$
.
$D_{s+1}$
.
Now the verification. It is clear that D is a computable linear order. We need to make sure it has the right order type. At each stage we densify around the points that are not part of a block, so between adjacent blocks we must have order type
![]() $\eta $
.
$\eta $
.
Claim 2.2.1. For every block
![]() $c\in L$
there is a unique block
$c\in L$
there is a unique block
![]() $b\in D$
that has the same length as c.
$b\in D$
that has the same length as c.
Proof Let
![]() $n=\max _{\mathbb {N}}(c)+1$
. There is a stage t such that for all
$n=\max _{\mathbb {N}}(c)+1$
. There is a stage t such that for all
![]() $s\ge t$
,
$s\ge t$
,
![]() $B_s\restriction {n}= B$
and
$B_s\restriction {n}= B$
and
![]() $<_s\restriction n=<_L\restriction n$
. At this stage t there will be a b such that
$<_s\restriction n=<_L\restriction n$
. At this stage t there will be a b such that
![]() $f_t(b)=\min _{\mathbb {N}}(c)$
. By our choice of t we have
$f_t(b)=\min _{\mathbb {N}}(c)$
. By our choice of t we have
![]() $f_s(b)=\min _{\mathbb {N}}(c)$
and
$f_s(b)=\min _{\mathbb {N}}(c)$
and
![]() $|b|\ge |c|$
for all
$|b|\ge |c|$
for all
![]() $s\ge t$
as there can be no reason to destroy b and we will never see any number smaller than n leave c.
$s\ge t$
as there can be no reason to destroy b and we will never see any number smaller than n leave c.
Given any
![]() $s>t$
and
$s>t$
and
![]() $m=\min _{\mathbb {N}}\{x\ge _{\mathbb {N}} n: \exists r>s[B_r(f_r(b),x)]\}$
there is a stage
$m=\min _{\mathbb {N}}\{x\ge _{\mathbb {N}} n: \exists r>s[B_r(f_r(b),x)]\}$
there is a stage
![]() $r>s$
such that
$r>s$
such that
![]() $ B_r(f_r(b),x)\land \neg B_{r+1}(f_{r+1}(b),x)$
. So at stage
$ B_r(f_r(b),x)\land \neg B_{r+1}(f_{r+1}(b),x)$
. So at stage
![]() $r+1$
we will have
$r+1$
we will have
![]() $|b|=|c|$
and as s is arbitrary, we have
$|b|=|c|$
and as s is arbitrary, we have
![]() $|b|\le |c|$
in D.
$|b|\le |c|$
in D.
Claim 2.2.2. For every block
![]() $b\in D$
there is a block
$b\in D$
there is a block
![]() $c\in L$
and t such that
$c\in L$
and t such that
![]() $|b|=|c|$
and for all
$|b|=|c|$
and for all
![]() $s\ge t$
,
$s\ge t$
,
![]() $f_s(b)=\min (c)$
. Furthermore, if
$f_s(b)=\min (c)$
. Furthermore, if
![]() $b_i<_D b_j$
then for the corresponding blocks
$b_i<_D b_j$
then for the corresponding blocks
![]() $c_i,c_j\in L$
we have
$c_i,c_j\in L$
we have
![]() $c_i<_L c_j$
.
$c_i<_L c_j$
.
Proof Consider a block b. Suppose
![]() $f_s(b)=n$
and
$f_s(b)=n$
and
![]() $f_t(b)=m$
for
$f_t(b)=m$
for
![]() $s<t$
. Then it must be that
$s<t$
. Then it must be that
![]() $f_s(b)\ge f_t(b)$
. So
$f_s(b)\ge f_t(b)$
. So
![]() $\lim _s f_s(b)$
exists. If
$\lim _s f_s(b)$
exists. If
![]() $x=\lim _s f_s(b)$
and c is the block of x in L then by the same argument as above we have that
$x=\lim _s f_s(b)$
and c is the block of x in L then by the same argument as above we have that
![]() $|b|=|c|$
.
$|b|=|c|$
.
If
![]() $x=\lim _s f_s(b_i)$
and
$x=\lim _s f_s(b_i)$
and
![]() $y=\lim _s f_s(b_j)$
and
$y=\lim _s f_s(b_j)$
and
![]() $b_i<_D b_j$
then
$b_i<_D b_j$
then
![]() $x<_L y$
as otherwise we would have removed one of the blocks.
$x<_L y$
as otherwise we would have removed one of the blocks.
So we can see that there is an order preserving bijection F from the blocks of D to the blocks of L with
![]() $|b|=|F(b)|$
. Hence the order type of D is the same as that of L.
$|b|=|F(b)|$
. Hence the order type of D is the same as that of L.
From the construction, if a point is removed from a block then it is never put back in a block at a later stage. So
![]() $\mathbf {0}'$
can compute the set of points in D that are not in blocks. As D is computable,
$\mathbf {0}'$
can compute the set of points in D that are not in blocks. As D is computable,
![]() $\mathbf {0}'$
can also compute the successor relation on D. From both of these,
$\mathbf {0}'$
can also compute the successor relation on D. From both of these,
![]() $\mathbf {0}'$
can compute the block relation.
$\mathbf {0}'$
can compute the block relation.
Theorem 2.2 is not quite what we would like as it requires the block relation to be
![]() $\mathbf {0}'$
-computable. However, this is a property that occurs if the blocks are created in isolation and never merged. This is precisely what happens in the constructions given in the proofs of the characterizations of
$\mathbf {0}'$
-computable. However, this is a property that occurs if the blocks are created in isolation and never merged. This is precisely what happens in the constructions given in the proofs of the characterizations of
![]() $\eta $
-representable and increasingly
$\eta $
-representable and increasingly
![]() $\eta $
-representable sets.
$\eta $
-representable sets.
Theorem 2.3. A set A is in
![]() $\mathbf {SSILM}(\mathbb {Q})$
if and only if there is a strong
$\mathbf {SSILM}(\mathbb {Q})$
if and only if there is a strong
![]() $\eta $
-s-representation with computable block relation.
$\eta $
-s-representation with computable block relation.
Proof For the left to right direction we observe that the usual construction (unrelativizing the one given in [Reference Kalimullin, Khoussainov and Melnikov8]) has computable block relation as the blocks that are created are never merged.
For the other direction, since we can compute if two blocks are actually the same block we can make sure we only assign one follower to each block.
By combining Theorems 2.3 and 2.2 we get a characterization of
![]() $\mathbf {SSILM}^{\mathbf {0}'}(\mathbb {Q})$
in terms of computable
$\mathbf {SSILM}^{\mathbf {0}'}(\mathbb {Q})$
in terms of computable
![]() $\eta $
-representations:
$\eta $
-representations:
Corollary 2.4. A set A is in
![]() $ \mathbf {SSILM}^{\mathbf {0}'}(\mathbb {Q})$
if and only if there is a strong
$ \mathbf {SSILM}^{\mathbf {0}'}(\mathbb {Q})$
if and only if there is a strong
![]() $\eta $
-representation of A with
$\eta $
-representation of A with
![]() $\mathbf {0}'$
-computable block relation.
$\mathbf {0}'$
-computable block relation.
Theorem 1.13 states that there are strongly
![]() $\eta $
-representable sets which are not in
$\eta $
-representable sets which are not in
![]() $\mathbf {SSILM}^{\mathbf {0}'}(\mathbb {Q})$
, so as a result any characterization of the sets with strong
$\mathbf {SSILM}^{\mathbf {0}'}(\mathbb {Q})$
, so as a result any characterization of the sets with strong
![]() $\eta $
-representations must involve merging blocks as part of the construction.
$\eta $
-representations must involve merging blocks as part of the construction.
3 Connected approximations
The limit lemma says that we can approximate any
![]() $\Delta ^0_2$
set A with a computable sequence
$\Delta ^0_2$
set A with a computable sequence
![]() $(A_n){}_{n}$
such that
$(A_n){}_{n}$
such that
![]() $A(x)=\lim _n A_n(x)$
. Limitwise monotonic functions are one way of building on this idea. From what we have seen, the problem with trying to use these to characterize strongly
$A(x)=\lim _n A_n(x)$
. Limitwise monotonic functions are one way of building on this idea. From what we have seen, the problem with trying to use these to characterize strongly
![]() $\eta $
-representable sets is that each limit of a sequence
$\eta $
-representable sets is that each limit of a sequence
![]() $F(q)= \lim _{s} f(q,s)$
is taken in isolation, and there is no natural way of merging sequences. So we propose a different way of approximating sets that captures the idea of merging sequences.
$F(q)= \lim _{s} f(q,s)$
is taken in isolation, and there is no natural way of merging sequences. So we propose a different way of approximating sets that captures the idea of merging sequences.
Definition 3.1. A connected approximation to a set A is a sequence of finite functions
![]() $(c_n)_n$
with associated sequences of finite sets
$(c_n)_n$
with associated sequences of finite sets
![]() $(A_{n,m})_m$
that satisfy the following:
$(A_{n,m})_m$
that satisfy the following:
-
1.
 $\mathrm {range}(c_n)\subseteq \mathrm {dom}(c_{n+1})$
for all n.
$\mathrm {range}(c_n)\subseteq \mathrm {dom}(c_{n+1})$
for all n. -
2.
 $A_{n,0}:=\mathrm {dom}(c_n)$
,
$A_{n,0}:=\mathrm {dom}(c_n)$
,
 $A_{n,m+1}:= c_{n+m}(A_{n,m})$
.
$A_{n,m+1}:= c_{n+m}(A_{n,m})$
. -
3. The limit
 $A_{n,\omega }:=\lim _m A_{n,m}$
always exists.
$A_{n,\omega }:=\lim _m A_{n,m}$
always exists. -
4.
 $A=\cup _n A_{n,\omega }$
.
$A=\cup _n A_{n,\omega }$
.
We can assume each
![]() $c_n$
is coded by a canonical index for the finite set of its graph
$c_n$
is coded by a canonical index for the finite set of its graph
![]() $\{\langle x, c_n(x)\rangle : x\in \mathrm {dom}(c_n)\}$
, so we can say a connected approximation
$\{\langle x, c_n(x)\rangle : x\in \mathrm {dom}(c_n)\}$
, so we can say a connected approximation
![]() $(c_n)_n$
is computable if the corresponding sequence of indices is computable.
$(c_n)_n$
is computable if the corresponding sequence of indices is computable.
We call a connected approximation
![]() $(c_n)_n$
monotonic if
$(c_n)_n$
monotonic if
![]() $c_n(x)\ge x$
for each n and
$c_n(x)\ge x$
for each n and
![]() $x\in \mathrm {dom}(c_n)$
, and order preserving if each
$x\in \mathrm {dom}(c_n)$
, and order preserving if each
![]() $c_n$
preserves
$c_n$
preserves
![]() $\le $
. We use the acronym MOP to denote monotonic and order preserving.
$\le $
. We use the acronym MOP to denote monotonic and order preserving.
We give characterizations of all of the existing classes described so far using connected approximations.
Theorem 3.2. For a set A we have the following characterizations.
-
1. A has a computable connected approximation if and only if A is
 $\Sigma ^0_2$
.
$\Sigma ^0_2$
. -
2. A has a computable monotonic connected approximation if and only if A is the range of a computable limitwise monotonic function.
-
3. A has a computable MOP connected approximation if and only if
 $A\in \mathbf {SILM}(\mathbb {Q})$
.
$A\in \mathbf {SILM}(\mathbb {Q})$
. -
4. A has a computable MOP connected approximation where each
 $c_n$
is injective if and only if
$c_n$
is injective if and only if
 $A\in \mathbf {SSILM}(\mathbb {Q})$
.
$A\in \mathbf {SSILM}(\mathbb {Q})$
.
Proof of (1) and (2) We will handle the first two statements together. Given a
![]() $\Sigma ^0_2$
set A we can assume
$\Sigma ^0_2$
set A we can assume
![]() $A=\mathrm {range}(F)$
for
$A=\mathrm {range}(F)$
for
![]() $F(n)=\lim _{s} f(n,s)$
where f is computable. Then we can define a connected approximation of
$F(n)=\lim _{s} f(n,s)$
where f is computable. Then we can define a connected approximation of
![]() $A=\mathrm {range}(F)$
as follows. Let
$A=\mathrm {range}(F)$
as follows. Let
![]() $\mathrm {dom}(c_n)=\{f(x,n): x< n\}$
and define
$\mathrm {dom}(c_n)=\{f(x,n): x< n\}$
and define
![]() $c_n(y)=f(x,n+1)$
where x is least such that
$c_n(y)=f(x,n+1)$
where x is least such that
![]() $f(x,n)=y$
. Clearly
$f(x,n)=y$
. Clearly
![]() $(c_n)_n$
is computable and
$(c_n)_n$
is computable and
![]() $\mathrm {range}(c_n)\subseteq \mathrm {dom}(c_{n+1})$
. For each
$\mathrm {range}(c_n)\subseteq \mathrm {dom}(c_{n+1})$
. For each
![]() $n,m$
we have that
$n,m$
we have that
![]() $A_{n,m}=f(B_{n,m},n+m)$
for some
$A_{n,m}=f(B_{n,m},n+m)$
for some
![]() $B_{n,m}\subseteq n$
. We take the
$B_{n,m}\subseteq n$
. We take the
![]() $B_{n,m}$
which minimizes
$B_{n,m}$
which minimizes
![]() $\sum _{x\in B_{n,m}}x$
. By construction
$\sum _{x\in B_{n,m}}x$
. By construction
![]() $\sum _{x\in B_{n,m}}x\ge \sum _{x\in B_{n,m+11}}$
and so the limit
$\sum _{x\in B_{n,m}}x\ge \sum _{x\in B_{n,m+11}}$
and so the limit
![]() $B_{n,\omega }:=\lim _{m} B_{n,m}$
exists. Hence
$B_{n,\omega }:=\lim _{m} B_{n,m}$
exists. Hence
![]() $A_{n,\omega }=F(B_{n,\omega })$
, so we have
$A_{n,\omega }=F(B_{n,\omega })$
, so we have
![]() $(c_n){}_{n}$
is a connected approximation of a subset of A. Consider an
$(c_n){}_{n}$
is a connected approximation of a subset of A. Consider an
![]() $n\in \omega $
. Let
$n\in \omega $
. Let
![]() $t> n$
be a stage after which
$t> n$
be a stage after which
![]() $f(m,s)=F(m)$
for all
$f(m,s)=F(m)$
for all
![]() $s\ge t, m\le n$
. Then
$s\ge t, m\le n$
. Then
![]() $F[n]\subseteq A_{t,0}$
, so
$F[n]\subseteq A_{t,0}$
, so
![]() $F[n]\subseteq A_{t,\omega }$
. So
$F[n]\subseteq A_{t,\omega }$
. So
![]() $(c_n)_n$
is a connected approximation of A. Notice that if
$(c_n)_n$
is a connected approximation of A. Notice that if
![]() $f(n,s)$
is monotonic in s then
$f(n,s)$
is monotonic in s then
![]() $(c_n)_n$
is also monotonic.
$(c_n)_n$
is also monotonic.
Now consider a computable connected approximation
![]() $(c_n)_n$
of a set A. We define a computable function
$(c_n)_n$
of a set A. We define a computable function
![]() $f:\omega ^2\rightarrow \omega $
as follows.
$f:\omega ^2\rightarrow \omega $
as follows.
![]() $f(n,0)=0$
,
$f(n,0)=0$
,
![]() $t_0=0$
. Define
$t_0=0$
. Define
![]() $f(n,s+1)$
as follows:
$f(n,s+1)$
as follows:
![]() $f(n,s+1)=c_s(f(n,s))$
if
$f(n,s+1)=c_s(f(n,s))$
if
![]() $n<t_s$
. Let
$n<t_s$
. Let
![]() $m_0,\dots , m_{k-1}$
list
$m_0,\dots , m_{k-1}$
list
![]() $\mathrm {range}(c_s)\setminus \mathrm {range}(c_s\circ c_{s-1})$
in order. Define
$\mathrm {range}(c_s)\setminus \mathrm {range}(c_s\circ c_{s-1})$
in order. Define
![]() $f(t_s+i,s+1)=m_i$
and
$f(t_s+i,s+1)=m_i$
and
![]() $t_{s+1}=t_s +k$
. For
$t_{s+1}=t_s +k$
. For
![]() $n\ge t_{s+1}$
let
$n\ge t_{s+1}$
let
![]() $f(n,s+1)=0$
. We have that
$f(n,s+1)=0$
. We have that
![]() $A_{n,m}=\{f(x,n+m): x\le t_{n}\}$
and so
$A_{n,m}=\{f(x,n+m): x\le t_{n}\}$
and so
![]() $\mathrm {range}(F\restriction t_n) = A_{n,\omega }$
and hence
$\mathrm {range}(F\restriction t_n) = A_{n,\omega }$
and hence
![]() $ \mathrm {range}(F)=A$
. Notice that if
$ \mathrm {range}(F)=A$
. Notice that if
![]() $(c_n){}_{n}$
is monotonic then F is limitwise monotonic.
$(c_n){}_{n}$
is monotonic then F is limitwise monotonic.
A similar idea works for characterizations (3) and (4), but when going from a connected approximation we need to choose rationals so that the order is preserved.
Now we give a characterization of strongly
![]() $\eta $
-s-representable sets using connected approximations. In a construction of a strong
$\eta $
-s-representable sets using connected approximations. In a construction of a strong
![]() $\eta $
-s-representation, blocks can do two things: they can grow and they can merge. Eventually they must stop doing either of these things, but we cannot put a computable bound of how late these actions take place. However, if two blocks are, in fact, different then we will see infinitely many points go in between them. Thus, if blocks merge at a late stage then the size of the resulting block should be very large. This is the main idea behind the formula in the following characterization and the proof.
$\eta $
-s-representation, blocks can do two things: they can grow and they can merge. Eventually they must stop doing either of these things, but we cannot put a computable bound of how late these actions take place. However, if two blocks are, in fact, different then we will see infinitely many points go in between them. Thus, if blocks merge at a late stage then the size of the resulting block should be very large. This is the main idea behind the formula in the following characterization and the proof.
Theorem 3.3. A set A has a strong
![]() $\eta $
-s-representation if and only if it has a computable MOP connected approximation where each
$\eta $
-s-representation if and only if it has a computable MOP connected approximation where each
![]() $c_n$
satisfies
$c_n$
satisfies
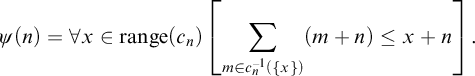 $$ \begin{align*} \psi(n)=\forall x\in \mathrm{range}(c_n)\left[\sum_{m\in c_n^{-1}(\{x\})}(m+n) \le x+n\right]. \end{align*} $$
$$ \begin{align*} \psi(n)=\forall x\in \mathrm{range}(c_n)\left[\sum_{m\in c_n^{-1}(\{x\})}(m+n) \le x+n\right]. \end{align*} $$
Proof Suppose we have a strong
![]() $\eta $
-s-representation L of A. We can assume that L has domain
$\eta $
-s-representation L of A. We can assume that L has domain
![]() $\omega $
and let
$\omega $
and let
![]() $L_s=L\restriction s$
. Let
$L_s=L\restriction s$
. Let
![]() $B_s$
be the blocks of
$B_s$
be the blocks of
![]() $L_s$
according to
$L_s$
according to
![]() $S_L$
. For blocks
$S_L$
. For blocks
![]() $b,c\in B_s$
and
$b,c\in B_s$
and
![]() $t\ge s$
we use
$t\ge s$
we use
![]() $|b|_t$
to denote the size the block has in
$|b|_t$
to denote the size the block has in
![]() $L_t$
, and we use
$L_t$
, and we use
![]() $b<_t c$
and
$b<_t c$
and
![]() $b=_t c$
to denote the order of the, possibly merged, blocks in
$b=_t c$
to denote the order of the, possibly merged, blocks in
![]() $L_t$
.
$L_t$
.
We start with
![]() $c_0=\emptyset $
,
$c_0=\emptyset $
,
![]() $t_0=0$
. At stage s we assume we are given
$t_0=0$
. At stage s we assume we are given
![]() $\mathrm {dom}(c_s)$
,
$\mathrm {dom}(c_s)$
,
![]() $t_s$
and a block
$t_s$
and a block
![]() $b_s\in B_{t_s}$
. We assume that for any
$b_s\in B_{t_s}$
. We assume that for any
![]() $c, d\in B_{t_s}$
with
$c, d\in B_{t_s}$
with
![]() $c<_{t_s}d\le _{t_s} b$
we have
$c<_{t_s}d\le _{t_s} b$
we have
![]() $|c|_{t_s}<|d|_{t_s}$
and there are at least s many points between c and d in
$|c|_{t_s}<|d|_{t_s}$
and there are at least s many points between c and d in
![]() $L_{t_s}$
. We also assume
$L_{t_s}$
. We also assume
![]() $\mathrm {dom}(c_s)= \{|b|_{t_s} : b\in B_{t_s}\land b\le _{t_s} b_s\}$
.
$\mathrm {dom}(c_s)= \{|b|_{t_s} : b\in B_{t_s}\land b\le _{t_s} b_s\}$
.
We let
![]() $b_{s+1}=\max _{<_{t_s}} B_{t_s}$
. Search for a
$b_{s+1}=\max _{<_{t_s}} B_{t_s}$
. Search for a
![]() $t>t_s$
such that for every
$t>t_s$
such that for every
![]() $c,d\in B_t$
with
$c,d\in B_t$
with
![]() $c<_t d\le _t b_{s+1}$
we have
$c<_t d\le _t b_{s+1}$
we have
![]() $|c|_t<|d|_t$
and there are at least
$|c|_t<|d|_t$
and there are at least
![]() $s+1$
many points between c and d in
$s+1$
many points between c and d in
![]() $L_{t_s}$
. The fact that L is a strong
$L_{t_s}$
. The fact that L is a strong
![]() $\eta $
-s-representation guarantees that we will find such a t. We let
$\eta $
-s-representation guarantees that we will find such a t. We let
![]() $t_{s+1}=t$
and
$t_{s+1}=t$
and
![]() $\mathrm {dom}(c_{s+1})=\{|b|_{t} : b\in B_{t}\land b\le _{t} b_{s+1}\}$
. We define
$\mathrm {dom}(c_{s+1})=\{|b|_{t} : b\in B_{t}\land b\le _{t} b_{s+1}\}$
. We define
![]() $c_s$
as follows. For
$c_s$
as follows. For
![]() $d\le _{t_s} b_s$
we set
$d\le _{t_s} b_s$
we set
![]() $c_s(|d|_{t_s})=|d|_t$
. This clearly gives
$c_s(|d|_{t_s})=|d|_t$
. This clearly gives
![]() $\mathrm {range}(c_s)\subseteq \mathrm {dom}(c_{s+1})$
. This completes the construction.
$\mathrm {range}(c_s)\subseteq \mathrm {dom}(c_{s+1})$
. This completes the construction.
Now we need to check that
![]() $c_s$
is MOP and meets the condition
$c_s$
is MOP and meets the condition
![]() $\psi $
. If
$\psi $
. If
![]() $|d|_{t_s}< |c|_{t_s}$
for
$|d|_{t_s}< |c|_{t_s}$
for
![]() $d,c<_{t_s} b_s$
then we have that
$d,c<_{t_s} b_s$
then we have that
![]() $d<_{t_s} c$
, so
$d<_{t_s} c$
, so
![]() $d\le _t c$
and
$d\le _t c$
and
![]() $|d|_t\le |c|_t$
. Thus
$|d|_t\le |c|_t$
. Thus
![]() $c_s$
preserves
$c_s$
preserves
![]() $\le $
. Since L is a strong
$\le $
. Since L is a strong
![]() $\eta $
-s-representation, we have that
$\eta $
-s-representation, we have that
![]() $|d|_n\le |d|_m$
for
$|d|_n\le |d|_m$
for
![]() $n\le m$
, and so
$n\le m$
, and so
![]() $c_s$
is monotonic. If we combine this with the fact that there are s many points between relevant blocks in
$c_s$
is monotonic. If we combine this with the fact that there are s many points between relevant blocks in
![]() $B_{t_s}$
we have that if
$B_{t_s}$
we have that if
![]() $d_1<_{t_s}\dots <_{t_s} d_n\le _{t_s}b_s$
but
$d_1<_{t_s}\dots <_{t_s} d_n\le _{t_s}b_s$
but
![]() $d_1=_t\dots =_t d_n$
then we have
$d_1=_t\dots =_t d_n$
then we have
![]() $|d_i|_t+s \ge \sum _{i=1}^n (|d_i|_{t_s} +s)$
. So we can conclude that
$|d_i|_t+s \ge \sum _{i=1}^n (|d_i|_{t_s} +s)$
. So we can conclude that
![]() $c_n$
meets the condition
$c_n$
meets the condition
![]() $\psi $
.
$\psi $
.
All that is left to check is that the limits exist and that they give us A. We have that
![]() $A_{n,m}=\{|d|_{t_{n+m}}: d\in B_{t_n}, d\le b_n\}$
. Since
$A_{n,m}=\{|d|_{t_{n+m}}: d\in B_{t_n}, d\le b_n\}$
. Since
![]() $B_{t_n}$
is a finite set and each block in
$B_{t_n}$
is a finite set and each block in
![]() $B_{t_n}$
only changes size finitely often, we have that the limit
$B_{t_n}$
only changes size finitely often, we have that the limit
![]() $A_{n,\omega }$
exists and
$A_{n,\omega }$
exists and
![]() $A_{n,\omega }\subseteq A$
. On the other hand, every
$A_{n,\omega }\subseteq A$
. On the other hand, every
![]() $d\in B_L$
is in some
$d\in B_L$
is in some
![]() $B_n$
, so the there is a stage s such that
$B_n$
, so the there is a stage s such that
![]() $t_s>n$
and then we have
$t_s>n$
and then we have
![]() $|d|_{t_{s+1}}\in \mathrm {dom}(c_{s+1})$
. Thus
$|d|_{t_{s+1}}\in \mathrm {dom}(c_{s+1})$
. Thus
![]() $|d|\in A_{s+1,\omega }$
. So we have that
$|d|\in A_{s+1,\omega }$
. So we have that
![]() $A=\cup _n A_{n,\omega }$
and
$A=\cup _n A_{n,\omega }$
and
![]() $(c_n)_n$
is a connected approximation of A as desired.
$(c_n)_n$
is a connected approximation of A as desired.
Now for the other direction. Suppose we have a connected approximation
![]() $(c_n)_n$
of A satisfying the conditions of the theorem. We construct an
$(c_n)_n$
of A satisfying the conditions of the theorem. We construct an
![]() $\eta $
-s-representation as follows. The main idea is that at stage s we will have a linear order
$\eta $
-s-representation as follows. The main idea is that at stage s we will have a linear order
![]() $L_s$
with successor relation and blocks
$L_s$
with successor relation and blocks
![]() $B_s$
strictly ordered by size with s many points in between, and the sizes of blocks of
$B_s$
strictly ordered by size with s many points in between, and the sizes of blocks of
![]() $B_s$
are the members of
$B_s$
are the members of
![]() $\mathrm {dom}(c_s)$
.
$\mathrm {dom}(c_s)$
.
We define a computable function
![]() $H(L,c,m)$
that takes a finite linear order L with successor, a finite function c and a number m, and outputs a finite linear order D with successor extending L if it can. We assume that the blocks
$H(L,c,m)$
that takes a finite linear order L with successor, a finite function c and a number m, and outputs a finite linear order D with successor extending L if it can. We assume that the blocks
![]() $B_L$
are ordered by size the same way they are by
$B_L$
are ordered by size the same way they are by
![]() $<_L$
. We assume that
$<_L$
. We assume that
![]() $\{|b|: b\in B_L\}\subseteq \mathrm {dom}(c)$
. We build D in steps as follows. If
$\{|b|: b\in B_L\}\subseteq \mathrm {dom}(c)$
. We build D in steps as follows. If
![]() $c(|b|)=c(|d|)$
then we merge blocks b and d and all the points in between into one large block. This gives us a
$c(|b|)=c(|d|)$
then we merge blocks b and d and all the points in between into one large block. This gives us a
![]() $D_0$
that differs from L only in the successor. We then go through each block b of
$D_0$
that differs from L only in the successor. We then go through each block b of
![]() $D_0$
, and if d was a block of L and
$D_0$
, and if d was a block of L and
![]() $d\subseteq b$
then we possibly add points to the end of b so that
$d\subseteq b$
then we possibly add points to the end of b so that
![]() $|b|=c(|d|)$
. If we have
$|b|=c(|d|)$
. If we have
![]() $|b|>c(|d|)$
already then H fails. If H does not fail then this gives us
$|b|>c(|d|)$
already then H fails. If H does not fail then this gives us
![]() $D_1$
. Now, for each
$D_1$
. Now, for each
![]() $n\in \mathrm {range}(c) \setminus \{|b|: b\in B_{D_1}\}$
, we add a new block of length n to
$n\in \mathrm {range}(c) \setminus \{|b|: b\in B_{D_1}\}$
, we add a new block of length n to
![]() $D_1$
, keeping the ordering of blocks by size. This gives us a
$D_1$
, keeping the ordering of blocks by size. This gives us a
![]() $D_2$
. Finally, between each pair of adjacent blocks in
$D_2$
. Finally, between each pair of adjacent blocks in
![]() $D_2$
, we add points in a dense way so that there are exactly m many points between them. This is D. If one of the assumptions was wrong then H fails, otherwise it succeeds, and D is a linear order with blocks ordered by size the sizes of which are
$D_2$
, we add points in a dense way so that there are exactly m many points between them. This is D. If one of the assumptions was wrong then H fails, otherwise it succeeds, and D is a linear order with blocks ordered by size the sizes of which are
![]() $\mathrm {range}(c)$
, and there are exactly m many points between adjacent blocks.
$\mathrm {range}(c)$
, and there are exactly m many points between adjacent blocks.
We define our strong
![]() $\eta $
-s-representation to be
$\eta $
-s-representation to be
![]() $L=\bigcup _s L_s$
where
$L=\bigcup _s L_s$
where
![]() $L_0=\emptyset $
and
$L_0=\emptyset $
and
![]() $L_{s+1}=H(L_s,c_s, s+1)$
. From the definition of H and the fact that each
$L_{s+1}=H(L_s,c_s, s+1)$
. From the definition of H and the fact that each
![]() $c_n$
preserves
$c_n$
preserves
![]() $\le $
and satisfies
$\le $
and satisfies
![]() $\psi $
we can see, using an induction argument, that H will always succeed, so the
$\psi $
we can see, using an induction argument, that H will always succeed, so the
![]() $L_s$
are all well-defined. From the definition of H we can see that if two points are never part of the same block for some
$L_s$
are all well-defined. From the definition of H we can see that if two points are never part of the same block for some
![]() $L_s$
then there is a point in between them. So we have that the successor relation on L is
$L_s$
then there is a point in between them. So we have that the successor relation on L is
![]() $S_L=\bigcup _n S_{L_n}$
. So L is a computable linear with c.e. successor relation. As the successor relation of a computable linear order is always co-c.e. we have that
$S_L=\bigcup _n S_{L_n}$
. So L is a computable linear with c.e. successor relation. As the successor relation of a computable linear order is always co-c.e. we have that
![]() $S_L$
is computable.
$S_L$
is computable.
By construction we have that
![]() $A_{n,m}=\{|b|_{n+m}: b \text { is a block in } L_{n+1}\}$
, and for every block b in
$A_{n,m}=\{|b|_{n+m}: b \text { is a block in } L_{n+1}\}$
, and for every block b in
![]() $L_n$
,
$L_n$
,
![]() $c_m(|b|_m)=|b|_{m+1}$
. So we have that
$c_m(|b|_m)=|b|_{m+1}$
. So we have that
![]() $A_{n,\omega }=\{|b|_L: b \text { is a block in } L_n\}$
and L is an
$A_{n,\omega }=\{|b|_L: b \text { is a block in } L_n\}$
and L is an
![]() $\eta $
-s-representation of A. As the blocks of
$\eta $
-s-representation of A. As the blocks of
![]() $L_n$
are ordered by increasing size so too are the blocks of L, so L is a strong
$L_n$
are ordered by increasing size so too are the blocks of L, so L is a strong
![]() $\eta $
-s-representation of A.
$\eta $
-s-representation of A.
Note that if we replace
![]() $\psi (n)$
by the condition
$\psi (n)$
by the condition
![]() $\forall x\in \mathrm {dom}(c_n)[(\sum _{m\in c_n^{-1}(\{x\})} m+ f(n) \le x+f(n)]$
for any computable non-decreasing f with
$\forall x\in \mathrm {dom}(c_n)[(\sum _{m\in c_n^{-1}(\{x\})} m+ f(n) \le x+f(n)]$
for any computable non-decreasing f with
![]() $\lim _n f(n)=\omega $
then a slight modification of the arguments above should still work and we get another characterization. The relativized version of the proof with
$\lim _n f(n)=\omega $
then a slight modification of the arguments above should still work and we get another characterization. The relativized version of the proof with
![]() $\mathbf {0}'$
-computable connected approximation, does not necessarily build us a computable strong
$\mathbf {0}'$
-computable connected approximation, does not necessarily build us a computable strong
![]() $\eta $
-representation, so we do not have a characterization of the strongly
$\eta $
-representation, so we do not have a characterization of the strongly
![]() $\eta $
-representable sets.
$\eta $
-representable sets.
4 The many-one degrees of
 $\eta $
-representable sets
$\eta $
-representable sets
We know from Kach and Turetsky [Reference Kalimullin, Khoussainov and Melnikov8] that if
![]() $S\in \mathbf {SSILM}(\mathbb {Q})$
then S has a strong
$S\in \mathbf {SSILM}(\mathbb {Q})$
then S has a strong
![]() $\eta $
-s-representation. The following is a condition on S under which the converse holds.
$\eta $
-s-representation. The following is a condition on S under which the converse holds.
Theorem 4.1. Suppose
![]() $g:\omega \rightarrow \omega $
is a computable increasing function. If a set A has a strong
$g:\omega \rightarrow \omega $
is a computable increasing function. If a set A has a strong
![]() $\eta $
-s-representation and satisfies
$\eta $
-s-representation and satisfies
![]() $|A\cap g(n)|\ge n$
for all n then
$|A\cap g(n)|\ge n$
for all n then
![]() $A\in \mathbf {SSILM}(\mathbb {Q})$
.
$A\in \mathbf {SSILM}(\mathbb {Q})$
.
Proof The construction goes as follows. We use an enumeration of
![]() $L=\{x_i:i\in \omega \}$
, and at stage s we look at the maximal blocks of
$L=\{x_i:i\in \omega \}$
, and at stage s we look at the maximal blocks of
![]() $L_s$
. We pick rationals to represent the blocks with the idea that
$L_s$
. We pick rationals to represent the blocks with the idea that
![]() $F(r)$
is the size of the block represented by r, but the block that r represents may change when blocks change. To keep track of what blocks rationals follow we will use a sequence of helper functions
$F(r)$
is the size of the block represented by r, but the block that r represents may change when blocks change. To keep track of what blocks rationals follow we will use a sequence of helper functions
![]() $h_s:\mathbb {Q}\rightarrow B_{t_s}$
with
$h_s:\mathbb {Q}\rightarrow B_{t_s}$
with
![]() $\mathrm {dom}(h_s)=\{r: f(r,s)>0\}$
. Once we see a block b appear in
$\mathrm {dom}(h_s)=\{r: f(r,s)>0\}$
. Once we see a block b appear in
![]() $L_s$
it can only grow, so it will remain a block in
$L_s$
it can only grow, so it will remain a block in
![]() $L_t$
for
$L_t$
for
![]() $t>s$
. Like we did in the proof of Theorem 3.3 we will use
$t>s$
. Like we did in the proof of Theorem 3.3 we will use
![]() $|b|_t$
,
$|b|_t$
,
![]() $b=_t c$
and
$b=_t c$
and
![]() $b<_t c$
to denote the size and order of the blocks from
$b<_t c$
to denote the size and order of the blocks from
![]() $L_s$
according to
$L_s$
according to
![]() $L_t$
. We let
$L_t$
. We let
![]() $B_t$
be the set of blocks from
$B_t$
be the set of blocks from
![]() $L_t$
.
$L_t$
.
At stage
![]() $0$
we start with
$0$
we start with
![]() $f(r,0)=0$
for all
$f(r,0)=0$
for all
![]() $r\in \mathbb {Q}$
and
$r\in \mathbb {Q}$
and
![]() $t_0=0$
. At stage s let
$t_0=0$
. At stage s let
![]() $b=\max (B_{t_s})$
. Let
$b=\max (B_{t_s})$
. Let
![]() $t_{s+1}=t$
be the least stage
$t_{s+1}=t$
be the least stage
![]() $t>t_s$
such that for each
$t>t_s$
such that for each
![]() $c<_t d\le _t b$
in
$c<_t d\le _t b$
in
![]() $B_{t}$
we have that
$B_{t}$
we have that
![]() $|c|_t <|d|_t$
and there are at least
$|c|_t <|d|_t$
and there are at least
![]() $g(|c|_t+|d|_t)$
many points between c and d in
$g(|c|_t+|d|_t)$
many points between c and d in
![]() $L_t$
, and furthermore for all n such that
$L_t$
, and furthermore for all n such that
![]() $g(n)\le |b|_t+1$
we have
$g(n)\le |b|_t+1$
we have
![]() $|\{c\in B_t: c\le _t b\land |c|< g(n)\}|\ge n$
. As L is an
$|\{c\in B_t: c\le _t b\land |c|< g(n)\}|\ge n$
. As L is an
![]() $\eta $
-s-representation of A there must be such a t.
$\eta $
-s-representation of A there must be such a t.
Let
![]() $r_0<\dots <r_{n-1}$
be the domain of
$r_0<\dots <r_{n-1}$
be the domain of
![]() $h_s$
; we begin defining
$h_s$
; we begin defining
![]() $h_{s+1}$
as follows. Let
$h_{s+1}$
as follows. Let
![]() $h_{s+1}(r_0)$
be the smallest block
$h_{s+1}(r_0)$
be the smallest block
![]() $c_0\in B_t$
such that
$c_0\in B_t$
such that
![]() $c_0\le _t h_{s}(r_0)\land |c_0|_t\ge f(r_0,s)$
. Let
$c_0\le _t h_{s}(r_0)\land |c_0|_t\ge f(r_0,s)$
. Let
![]() $h_{s+1}(r_i)$
be the smallest block
$h_{s+1}(r_i)$
be the smallest block
![]() $c_i\in B_t$
such that
$c_i\in B_t$
such that
![]() $h_{s+1}(r_{i-1})<_t c_i\le _t h_{s}(r_i)\land |c_i|_t\ge f(r_i,s)$
.
$h_{s+1}(r_{i-1})<_t c_i\le _t h_{s}(r_i)\land |c_i|_t\ge f(r_i,s)$
.
For each block
![]() $c\le _t b$
that is not in
$c\le _t b$
that is not in
![]() $\mathrm {range}(h_{s+1})$
we pick a rational
$\mathrm {range}(h_{s+1})$
we pick a rational
![]() $r_c$
and set
$r_c$
and set
![]() $h_{s+1}(r_c)=c$
so that
$h_{s+1}(r_c)=c$
so that
![]() $h_{s+1}$
is order preserving and has image
$h_{s+1}$
is order preserving and has image
![]() $\{c\in B: c\le _t b\}$
. We define
$\{c\in B: c\le _t b\}$
. We define
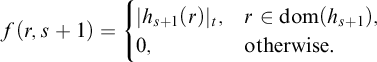 $$ \begin{align*}f(r,s+1)=\begin{cases} |h_{s+1}(r)|_t, & r\in \mathrm{dom}(h_{s+1}),\\ 0, & \text{otherwise}. \end{cases}\end{align*} $$
$$ \begin{align*}f(r,s+1)=\begin{cases} |h_{s+1}(r)|_t, & r\in \mathrm{dom}(h_{s+1}),\\ 0, & \text{otherwise}. \end{cases}\end{align*} $$
Now for the verification: first we need to show that the recursive definition of
![]() $h_{s+1}(r_i)$
actually works. Suppose it does not. Then let i be least such that we cannot find a block for
$h_{s+1}(r_i)$
actually works. Suppose it does not. Then let i be least such that we cannot find a block for
![]() $r_i$
.
$r_i$
.
![]() $|h_s(r_i)|_t\ge |h_s(r_i)|_{t_s}\ge f(r_i,s)$
so if
$|h_s(r_i)|_t\ge |h_s(r_i)|_{t_s}\ge f(r_i,s)$
so if
![]() $h_s(r_i)$
does not work then there must be some smaller
$h_s(r_i)$
does not work then there must be some smaller
![]() $r_j$
with
$r_j$
with
![]() $h_{s+1}(r_j)=h_s(r_i)$
. So
$h_{s+1}(r_j)=h_s(r_i)$
. So
![]() $i>0$
. We have
$i>0$
. We have
![]() $h_{s+1}(r_{i-1})\le _t h_s(r_{i-1})<_{t_s} h_{s}(r_i)$
, so it must be that
$h_{s+1}(r_{i-1})\le _t h_s(r_{i-1})<_{t_s} h_{s}(r_i)$
, so it must be that
![]() $h_s(r_{i-1})$
and
$h_s(r_{i-1})$
and
![]() $h_{s}(r_i)$
have merged. So
$h_{s}(r_i)$
have merged. So
![]() $|h_s(r_i)|_t> g(|h_s(r_{i-1})|_{t_s}+ |h_s(r_i)|_{t_s})$
. So by our choice of
$|h_s(r_i)|_t> g(|h_s(r_{i-1})|_{t_s}+ |h_s(r_i)|_{t_s})$
. So by our choice of
![]() $t_s$
we have at least
$t_s$
we have at least
![]() $|h_s(r_{i-1})|_{t_s}+ |h_s(r_i)|_{t_s}$
many blocks before
$|h_s(r_{i-1})|_{t_s}+ |h_s(r_i)|_{t_s}$
many blocks before
![]() $h_s(r_i)$
and at least
$h_s(r_i)$
and at least
![]() $|h_s(r_i)|_{t_s}$
have size at least
$|h_s(r_i)|_{t_s}$
have size at least
![]() $|h_s(r_{i-1})|_{t_s}$
. But
$|h_s(r_{i-1})|_{t_s}$
. But
![]() $i\le |h_s(r_i)|_{t_s}$
, so we would have chosen
$i\le |h_s(r_i)|_{t_s}$
, so we would have chosen
![]() $h_{s+1}(r_{i-1})$
to be one of these, a contradiction.
$h_{s+1}(r_{i-1})$
to be one of these, a contradiction.
From the definition of
![]() $h_s$
we can see that
$h_s$
we can see that
![]() $h_{s+1}(r)\le _L h_{s}(r)$
for each r and s, so as the blocks of L are well ordered,
$h_{s+1}(r)\le _L h_{s}(r)$
for each r and s, so as the blocks of L are well ordered,
![]() $\lim _s h_{s}(r)$
exists. From the definition of f we have that it is limitwise monotonic and
$\lim _s h_{s}(r)$
exists. From the definition of f we have that it is limitwise monotonic and
![]() $F(r)=|\lim _s h_s(r)|_L$
. So
$F(r)=|\lim _s h_s(r)|_L$
. So
![]() $\mathrm {range}(F)\subseteq S$
. If b is a block of L then after some stage t, all of b is in
$\mathrm {range}(F)\subseteq S$
. If b is a block of L then after some stage t, all of b is in
![]() $L_t$
as well as all smaller blocks. So at some stage s,
$L_t$
as well as all smaller blocks. So at some stage s,
![]() $t_s>t$
, so at stage
$t_s>t$
, so at stage
![]() $s+1$
we have an r such that
$s+1$
we have an r such that
![]() $h_{s+1}(r)=b$
and for any
$h_{s+1}(r)=b$
and for any
![]() $n>s$
we have
$n>s$
we have
![]() $h_n(r)= b$
as the blocks in that part of the linear order no longer change.
$h_n(r)= b$
as the blocks in that part of the linear order no longer change.
So
![]() $S=\mathrm {range}(F)$
as desired.
$S=\mathrm {range}(F)$
as desired.
Relativizing we get the following:
Corollary 1.14. Suppose
![]() $g:\omega \rightarrow \omega $
is a
$g:\omega \rightarrow \omega $
is a
![]() $\mathbf {0}'$
-computable increasing function. If a set A has a strong
$\mathbf {0}'$
-computable increasing function. If a set A has a strong
![]() $\eta $
-representation and satisfies
$\eta $
-representation and satisfies
![]() $|A\cap g(n)|\ge n$
for all n then
$|A\cap g(n)|\ge n$
for all n then
![]() $A\in \mathbf {SSILM}^{0'}(\mathbb {Q})$
.
$A\in \mathbf {SSILM}^{0'}(\mathbb {Q})$
.
This means that for dense enough sets, the notions of
![]() $\Delta ^0_2$
strong
$\Delta ^0_2$
strong
![]() $\eta $
-s-representation, strong
$\eta $
-s-representation, strong
![]() $\eta $
-representation and support strictly increasing limitwise monotonic on
$\eta $
-representation and support strictly increasing limitwise monotonic on
![]() $\mathbb {Q}$
all coincide.
$\mathbb {Q}$
all coincide.
Note that we cannot use Theorem 4.1 to give a characterization of
![]() $\mathbf {SSILM}(\mathbb {Q})$
as there are sparse sets in
$\mathbf {SSILM}(\mathbb {Q})$
as there are sparse sets in
![]() $\mathbf {SSILM}(\mathbb {Q})$
. For instance consider the function
$\mathbf {SSILM}(\mathbb {Q})$
. For instance consider the function
![]() $F(n)=n+\sum _{e\in \emptyset '\cap n} h(e)$
where
$F(n)=n+\sum _{e\in \emptyset '\cap n} h(e)$
where
![]() $h(e)$
is the least s such that
$h(e)$
is the least s such that
![]() $\varphi _{e,s}(e){\downarrow }$
. Then as F cannot be computably bounded,
$\varphi _{e,s}(e){\downarrow }$
. Then as F cannot be computably bounded,
![]() $S=\mathrm {range}(F)$
would not meet the condition
$S=\mathrm {range}(F)$
would not meet the condition
![]() $|S\cap g(n)|\ge n$
for all n for any computable g, but by definition it is clearly limitwise monotonic and increasing, so
$|S\cap g(n)|\ge n$
for all n for any computable g, but by definition it is clearly limitwise monotonic and increasing, so
![]() $S\in \mathbf {SSILM}(\mathbb {Q})$
.
$S\in \mathbf {SSILM}(\mathbb {Q})$
.
We can, however, use Theorem 4.1 to characterize the degrees of sets with computable strong
![]() $\eta $
-representations.
$\eta $
-representations.
Theorem 4.2. If
![]() $\mathbf {a}$
is the m-degree of a set with a strong
$\mathbf {a}$
is the m-degree of a set with a strong
![]() $\eta $
-s-representation then there is
$\eta $
-s-representation then there is
![]() $S\in \mathbf {a}$
such that
$S\in \mathbf {a}$
such that
![]() $S\in \mathbf {SSILM}(\mathbb {Q})$
.
$S\in \mathbf {SSILM}(\mathbb {Q})$
.
To prove this we use the following lemma.
Lemma 4.3. If A is a set with a strong
![]() $\eta $
-s-representation then
$\eta $
-s-representation then
![]() $A\oplus \omega $
also has a strong
$A\oplus \omega $
also has a strong
![]() $\eta $
-s-representation.
$\eta $
-s-representation.
Proof Suppose that A is a set with a strong
![]() $\eta $
-s-representation. Let
$\eta $
-s-representation. Let
![]() $(c_n)_n$
be a computable MOP connected approximation of A satisfying condition
$(c_n)_n$
be a computable MOP connected approximation of A satisfying condition
![]() $\psi $
of Theorem 3.3. We build an connected approximation
$\psi $
of Theorem 3.3. We build an connected approximation
![]() $(d_n)_n$
of
$(d_n)_n$
of
![]() $A\oplus \omega $
satisfying
$A\oplus \omega $
satisfying
![]() $\psi $
as follows. The first idea is to use
$\psi $
as follows. The first idea is to use
![]() $c_m$
with m much larger than n to build
$c_m$
with m much larger than n to build
![]() $d_n$
. We want m to be large enough that when we see
$d_n$
. We want m to be large enough that when we see
![]() $c_m(x)=c_m(y)$
we can merge the corresponding numbers
$c_m(x)=c_m(y)$
we can merge the corresponding numbers
![]() $2x,2y\in \mathrm {dom}(d_n)$
without violating
$2x,2y\in \mathrm {dom}(d_n)$
without violating
![]() $\psi $
. The second idea is that when we see
$\psi $
. The second idea is that when we see
![]() $c_m(x)>x$
without any merging, we shift the representative of x in
$c_m(x)>x$
without any merging, we shift the representative of x in
![]() $\mathrm {dom}(d_n)$
to a lager number so that we can handle the case where the gaps between numbers shrink, i.e., when
$\mathrm {dom}(d_n)$
to a lager number so that we can handle the case where the gaps between numbers shrink, i.e., when
![]() $c_m(y)-c_m(x) < y-x$
for
$c_m(y)-c_m(x) < y-x$
for
![]() $y>x$
.
$y>x$
.
To start let
![]() $d_0=\emptyset $
and
$d_0=\emptyset $
and
![]() $m_0=0$
. We will ensure that
$m_0=0$
. We will ensure that
![]() $m_n> \sum _{x\in \mathrm {dom}(d_n)} (x+n)$
, and if
$m_n> \sum _{x\in \mathrm {dom}(d_n)} (x+n)$
, and if
![]() $2x\in \mathrm {range}(d_n)$
then
$2x\in \mathrm {range}(d_n)$
then
![]() $x\in \mathrm {range}(c_{m_n})$
. Given
$x\in \mathrm {range}(c_{m_n})$
. Given
![]() $d_n$
and
$d_n$
and
![]() $m_n$
, let
$m_n$
, let
![]() $N>m_n$
be the least number such that if
$N>m_n$
be the least number such that if
![]() $ x=\max (A_{m_n, N+1})$
then
$ x=\max (A_{m_n, N+1})$
then
![]() $N> 2x(2x+n+1)$
. Let
$N> 2x(2x+n+1)$
. Let
![]() $m_{n+1}=N$
. This will ensure that
$m_{n+1}=N$
. This will ensure that
![]() $m_{n+1}> \sum _{x\in \mathrm {dom}(d_{n+1})} (x+n+1)$
. There must be such an N as
$m_{n+1}> \sum _{x\in \mathrm {dom}(d_{n+1})} (x+n+1)$
. There must be such an N as
![]() $(c_n)_n$
is a valid connected approximation, so eventually x will stabilize. Let
$(c_n)_n$
is a valid connected approximation, so eventually x will stabilize. Let
![]() $c=c_{N}\circ \dots \circ c_{m_n+1}$
.
$c=c_{N}\circ \dots \circ c_{m_n+1}$
.
Let
![]() $z\in \mathrm {dom} (c)$
be the least such that there is
$z\in \mathrm {dom} (c)$
be the least such that there is
![]() $y>z$
,
$y>z$
,
![]() $c(z)=c(y)$
. For
$c(z)=c(y)$
. For
![]() $y\ge 2z\in \mathrm {range} (d_n)$
we define
$y\ge 2z\in \mathrm {range} (d_n)$
we define
![]() $d_{n+1}(y)= 2c(z)$
. By assumption on
$d_{n+1}(y)= 2c(z)$
. By assumption on
![]() $m_n$
, this will not violate condition
$m_n$
, this will not violate condition
![]() $\psi $
. If there is no such z then set
$\psi $
. If there is no such z then set
![]() $z=\max (\mathrm {dom}(c))+1$
. Now we define
$z=\max (\mathrm {dom}(c))+1$
. Now we define
![]() $d_{n+1}$
on values smaller than
$d_{n+1}$
on values smaller than
![]() $2z$
.
$2z$
.
Let
![]() $a_0,\dots ,a_{s-1}$
list the elements of
$a_0,\dots ,a_{s-1}$
list the elements of
![]() $(\mathrm {dom}(c)\oplus \omega )\cap 2z-1$
. Let
$(\mathrm {dom}(c)\oplus \omega )\cap 2z-1$
. Let
![]() $b_0,\dots , b_{s-1}$
list the first s elements of
$b_0,\dots , b_{s-1}$
list the first s elements of
![]() $\mathrm {range}(c)\oplus \omega $
. Note that
$\mathrm {range}(c)\oplus \omega $
. Note that
![]() $b_{s-1}<2c(z)$
if
$b_{s-1}<2c(z)$
if
![]() $c(z)$
is defined. We define
$c(z)$
is defined. We define
![]() $d_{n+1}(a_i)=b_i$
. This is definitely order preserving, and it is monotonic because c is injective and monotonic on
$d_{n+1}(a_i)=b_i$
. This is definitely order preserving, and it is monotonic because c is injective and monotonic on
![]() $\mathrm {dom}(c)\cap z$
. This completes the construction of
$\mathrm {dom}(c)\cap z$
. This completes the construction of
![]() $(d_n)_n$
.
$(d_n)_n$
.
Verification: By construction we can see that
![]() $(d_n){}_{n}$
is MOP and satisfies
$(d_n){}_{n}$
is MOP and satisfies
![]() $\psi $
; all that is left to check is that it is a connected approximation of
$\psi $
; all that is left to check is that it is a connected approximation of
![]() $A\oplus \omega $
. Let
$A\oplus \omega $
. Let
![]() $x\in \mathrm {dom}(d_n)$
and let
$x\in \mathrm {dom}(d_n)$
and let
![]() $2y$
be the least even number in
$2y$
be the least even number in
![]() $\mathrm {dom}(d_n)\setminus x$
. Following the construction we can see that
$\mathrm {dom}(d_n)\setminus x$
. Following the construction we can see that
![]() $d_n(x)\le d_n(2y)\le 2(c_{m_{n}}\circ \dots \circ c_{m_{n-1}+1})(y)$
. So if we repeat this then we can see that the limit of
$d_n(x)\le d_n(2y)\le 2(c_{m_{n}}\circ \dots \circ c_{m_{n-1}+1})(y)$
. So if we repeat this then we can see that the limit of
![]() $x,d_n(x),d_{n+1}(d_n(x)),\dots $
if it exists is less than the limit of
$x,d_n(x),d_{n+1}(d_n(x)),\dots $
if it exists is less than the limit of
![]() $2y,2c_{m_n}(y),2c_{m_n+1}(c_{m_n}(y)),\dots $
, so by monotonicity it exists. Thus
$2y,2c_{m_n}(y),2c_{m_n+1}(c_{m_n}(y)),\dots $
, so by monotonicity it exists. Thus
![]() $(d_n)_n$
is a valid connected approximation.
$(d_n)_n$
is a valid connected approximation.
Fix x. Let s be a stage at which
![]() $c_n\restriction x= c_s\restriction x$
for all
$c_n\restriction x= c_s\restriction x$
for all
![]() $n\ge s$
. Then by the construction we have that
$n\ge s$
. Then by the construction we have that
![]() $d_n\restriction 2x= d_s \restriction 2x$
for all
$d_n\restriction 2x= d_s \restriction 2x$
for all
![]() $n\ge s$
and
$n\ge s$
and
![]() $\mathrm {dom}(d_n)\cap 2x = (\mathrm {dom}(c_n)\cap x) \oplus x$
. So
$\mathrm {dom}(d_n)\cap 2x = (\mathrm {dom}(c_n)\cap x) \oplus x$
. So
![]() $(d_n)_n$
is a connected approximation of
$(d_n)_n$
is a connected approximation of
![]() $A\oplus \omega $
.
$A\oplus \omega $
.
This allows us to characterize the m-degrees of sets with strong
![]() $\eta $
-representations.
$\eta $
-representations.
Corollary 1.15. The following coincide.
-
• The m-degrees of sets with computable strong
 $\eta $
-representations.
$\eta $
-representations. -
• The m-degrees of sets in
 $\mathbf {SSILM}^{\mathbf {0}'}(\mathbb {Q})$
.
$\mathbf {SSILM}^{\mathbf {0}'}(\mathbb {Q})$
. -
• The m-degrees of sets with
 $\Delta ^0_2$
strong
$\Delta ^0_2$
strong
 $\eta $
-s-representations.
$\eta $
-s-representations.
5 Open questions
We can characterize the m-degrees of sets with strong
![]() $\eta $
-representations, but we leave open the following.
$\eta $
-representations, but we leave open the following.
Question 5.1. Is there a characterization of the sets with strong
![]() $\eta $
-representations that is not in terms of linear orders?
$\eta $
-representations that is not in terms of linear orders?
A related question is in regards to the sets with
![]() $\Delta ^0_2$
strong
$\Delta ^0_2$
strong
![]() $\eta $
-s-representations.
$\eta $
-s-representations.
Question 5.2. Is there a set with a
![]() $\Delta ^0_2$
strong
$\Delta ^0_2$
strong
![]() $\eta $
-s-representation, but no computable strong
$\eta $
-s-representation, but no computable strong
![]() $\eta $
-s-representation?
$\eta $
-s-representation?
A negative answer to Question 5.2 would give us an answer to Question 5.1, using the connected approximation characterization of sets with computable strong
![]() $\eta $
-s-representations.
$\eta $
-s-representations.
Acknowledgment
The author was partially supported by NSF Grant No. DMS-2053848.