Article contents
Categoricity transfer in simple finitary abstract elementary classes
Published online by Cambridge University Press: 12 March 2014
Abstract
We continue our study of finitary abstract elementary classes, defined in [7]. In this paper, we prove a categoricity transfer theorem for a case of simple finitary AECs. We introduce the concepts of weak κ-categoricity and f-primary models to the framework of ℵ0-stable simple finitary AECs with the extension property, whereby we gain the following theorem: Let (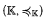 ) be a simple finitary AEC, weakly categorical in some uncountable κ. Then (
) be a simple finitary AEC, weakly categorical in some uncountable κ. Then (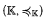 ) is weakly categorical in each λ ≥ min
) is weakly categorical in each λ ≥ min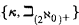 . If the class (
. If the class (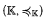 ) is also
) is also 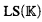 -tame, weak κ-categoricity is equivalent with κ-categoricity in the usual sense.
-tame, weak κ-categoricity is equivalent with κ-categoricity in the usual sense.
We also discuss the relation between finitary AECs and some other non-elementary frameworks and give several examples.
Information
- Type
- Research Article
- Information
- Copyright
- Copyright © Association for Symbolic Logic 2011
References
REFERENCES
- 8
- Cited by

