Article contents
CATEGORICAL SEMANTICS OF METRIC SPACES AND CONTINUOUS LOGIC
Published online by Cambridge University Press: 05 October 2020
Abstract
Using the category of metric spaces as a template, we develop a metric analogue of the categorical semantics of classical/intuitionistic logic, and show that the natural notion of predicate in this “continuous semantics” is equivalent to the a priori separate notion of predicate in continuous logic, a logic which is independently well-studied by model theorists and which finds various applications. We show this equivalence by exhibiting the real interval 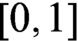 $[0,1]$ in the category of metric spaces as a “continuous subobject classifier” giving a correspondence not only between the two notions of predicate, but also between the natural notion of quantification in the continuous semantics and the existing notion of quantification in continuous logic.
$[0,1]$ in the category of metric spaces as a “continuous subobject classifier” giving a correspondence not only between the two notions of predicate, but also between the natural notion of quantification in the continuous semantics and the existing notion of quantification in continuous logic.
Along the way, we formulate what it means for a given category to behave like the category of metric spaces, and afterwards show that any such category supports the aforementioned continuous semantics. As an application, we show that categories of presheaves of metric spaces are examples of such, and in fact even possess continuous subobject classifiers.
Keywords
Information
- Type
- Articles
- Information
- Copyright
- © The Association for Symbolic Logic 2020
References
REFERENCES
- 1
- Cited by


