Article contents
CANTOR’S THEOREM MAY FAIL FOR FINITARY PARTITIONS
Published online by Cambridge University Press: 03 April 2024
Abstract
A partition is finitary if all its members are finite. For a set A, 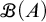 $\mathscr {B}(A)$ denotes the set of all finitary partitions of A. It is shown consistent with
$\mathscr {B}(A)$ denotes the set of all finitary partitions of A. It is shown consistent with  $\mathsf {ZF}$ (without the axiom of choice) that there exist an infinite set A and a surjection from A onto
$\mathsf {ZF}$ (without the axiom of choice) that there exist an infinite set A and a surjection from A onto 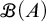 $\mathscr {B}(A)$. On the other hand, we prove in
$\mathscr {B}(A)$. On the other hand, we prove in  $\mathsf {ZF}$ some theorems concerning
$\mathsf {ZF}$ some theorems concerning 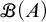 $\mathscr {B}(A)$ for infinite sets A, among which are the following:
$\mathscr {B}(A)$ for infinite sets A, among which are the following:
(1) If there is a finitary partition of A without singleton blocks, then there are no surjections from A onto
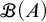 $\mathscr {B}(A)$ and no finite-to-one functions from
$\mathscr {B}(A)$ and no finite-to-one functions from 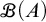 $\mathscr {B}(A)$ to A.
$\mathscr {B}(A)$ to A.(2) For all
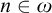 $n\in \omega $,
$n\in \omega $, 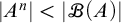 $|A^n|<|\mathscr {B}(A)|$.
$|A^n|<|\mathscr {B}(A)|$.(3)
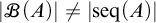 $|\mathscr {B}(A)|\neq |\mathrm {seq}(A)|$, where
$|\mathscr {B}(A)|\neq |\mathrm {seq}(A)|$, where 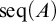 $\mathrm {seq}(A)$ is the set of all finite sequences of elements of A.
$\mathrm {seq}(A)$ is the set of all finite sequences of elements of A.
Information
- Type
- Article
- Information
- Copyright
- © The Author(s), 2024. Published by Cambridge University Press on behalf of The Association for Symbolic Logic
References
- 1
- Cited by


