Article contents
A boundedness lemma for iterations
Published online by Cambridge University Press: 12 March 2014
Extract
The purpose of this paper is to present a kind of boundedness lemma for direct limits of coarse structural mice, and to indicate some applications to descriptive set theory. For instance, this allows us to show that under large cardinal or determinacy assumptions there is no prewellorder ≤ of length 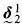 such that for some formula ψ and parameter z
such that for some formula ψ and parameter z
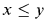
if and only if
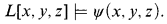
It is a peculiar experience to write up a result in this area. Following the work of Martin, Steel, Woodin, and other inner model theory experts, there is an enormous overhang of theorems and ideas, and it only takes one wandering pebble to restart the avalanche. For this reason I have chosen to center the exposition around the one pebble at 1.7 which I believe to be new. The applications discussed in section 2 involve routine modifications of known methods.
A detailed introduction to many of the techniques related to using the Martin-Steel inner model theory and Woodin's free extender algebra is given in the course of [1]. Certainly a familiarity with the Martin-Steel papers, [5] and [6], is a prerequisite, as is some knowledge of the free extender algebra. Probably anyone interested in this paper will already know the necessary descriptive set theory, most of which can be found in [4]. Discussion of earlier results in this direction can be found in [3] or [2].
Information
- Type
- Research Article
- Information
- Copyright
- Copyright © Association for Symbolic Logic 2001
References
REFERENCES
- 3
- Cited by

