Published online by Cambridge University Press: 19 June 2017
Given a countable o-minimal theory T, we characterize the Borel complexity of isomorphism for countable models of T up to two model-theoretic invariants. If T admits a nonsimple type, then it is shown to be Borel complete by embedding the isomorphism problem for linear orders into the isomorphism problem for models of T. This is done by constructing models with specific linear orders in the tail of the Archimedean ladder of a suitable nonsimple type.
If the theory admits no nonsimple types, then we use Mayer’s characterization of isomorphism for such theories to compute invariants for countable models. If the theory is small, then the invariant is real-valued, and therefore its isomorphism relation is smooth. If not, the invariant corresponds to a countable set of reals, and therefore the isomorphism relation is Borel equivalent to F 2.
Combining these two results, we conclude that 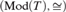 $\left( {{\rm{Mod}}\left( T \right), \cong } \right)$ is either maximally complicated or maximally uncomplicated (subject to completely general model-theoretic lower bounds based on the number of types and the number of countable models).
$\left( {{\rm{Mod}}\left( T \right), \cong } \right)$ is either maximally complicated or maximally uncomplicated (subject to completely general model-theoretic lower bounds based on the number of types and the number of countable models).