No CrossRef data available.
Article contents
Boolean operations, Borel sets, and Hausdorff's question
Published online by Cambridge University Press: 12 March 2014
Extract
The study of infinitary Boolean operations was undertaken by the early researchers of descriptive set theory soon after Suslin's discovery of the important 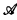 operation. The first attempt to lay down their theory in a systematic fashion was the work of Kantorovich and Livenson [5], where they call these the analytical operations. Earlier, Hausdorff had introduced the δs operations — essentially same as the monotoneω-ary Boolean operations, and Kolmogorov, independently of Hausdorff, had discovered the same objects, which were used in his study of the R operator.
operation. The first attempt to lay down their theory in a systematic fashion was the work of Kantorovich and Livenson [5], where they call these the analytical operations. Earlier, Hausdorff had introduced the δs operations — essentially same as the monotoneω-ary Boolean operations, and Kolmogorov, independently of Hausdorff, had discovered the same objects, which were used in his study of the R operator.
The ω-ary Boolean operations turned out to be closely related to most of the classical hierarchies over a fixed Polish space X, including, e. g., the Borel hierarchy (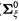 ), the difference hierarchies of Hausdorff (Dη(
), the difference hierarchies of Hausdorff (Dη(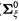 )), the C-hierarchy (Cξ) of Selivanovski, and the projective hierarchy (
)), the C-hierarchy (Cξ) of Selivanovski, and the projective hierarchy (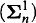 ): for each of these hierarchies, every level can be expressed as the range of an ω-ary Boolean operation applied to all possible sequences of open subsets of X. In the terminology of Dougherty [3], every level is “open-ω-Boolean” (if
): for each of these hierarchies, every level can be expressed as the range of an ω-ary Boolean operation applied to all possible sequences of open subsets of X. In the terminology of Dougherty [3], every level is “open-ω-Boolean” (if 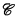 and
and 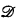 are collections of subsets of X and I is any set,
are collections of subsets of X and I is any set, 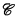 is said to be
is said to be 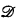 -I-Boolean if there exists an I-ary Boolean operation Φ such that
-I-Boolean if there exists an I-ary Boolean operation Φ such that 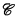 =
= 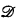 Φ, i. e.
Φ, i. e. 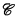 is the range of Φ restricted to all possible I-sequences of sets from
is the range of Φ restricted to all possible I-sequences of sets from 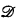 ). If in addition, the space X has a basis consisting of clopen sets, then the levels of the above hierarchies are also “clopen-ω-Boolean.”
). If in addition, the space X has a basis consisting of clopen sets, then the levels of the above hierarchies are also “clopen-ω-Boolean.”
Information
- Type
- Research Article
- Information
- Copyright
- Copyright © Association for Symbolic Logic 1996

