Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Harizanov, Valentina S.
1998.
Handbook of Recursive Mathematics - Volume 1: Recursive Model Theory.
Vol. 138,
Issue. ,
p.
3.
Knight, J.F.
1998.
Handbook of Recursive Mathematics - Volume 1: Recursive Model Theory.
Vol. 138,
Issue. ,
p.
289.
Cenzer, D.
and
Remmel, J.B.
1998.
Handbook of Recursive Mathematics - Volume 2: Recursive Algebra, Analysis and Combinatorics.
Vol. 139,
Issue. ,
p.
623.
Kalantari, I.
1998.
Handbook of Recursive Mathematics - Volume 1: Recursive Model Theory.
Vol. 138,
Issue. ,
p.
515.
Downey, R.G.
1998.
Handbook of Recursive Mathematics - Volume 2: Recursive Algebra, Analysis and Combinatorics.
Vol. 139,
Issue. ,
p.
823.
2000.
Computable Structures and the Hyperarithmetical Hierarchy.
Vol. 144,
Issue. ,
p.
323.
Harizanov, Valentina S.
2002.
Computability-Theoretic Complexity of Countable Structures.
Bulletin of Symbolic Logic,
Vol. 8,
Issue. 4,
p.
457.
Steiner, Rebecca M.
2012.
How the World Computes.
Vol. 7318,
Issue. ,
p.
696.
Montalban, A.
2012.
Counting the back-and-forth types.
Journal of Logic and Computation,
Vol. 22,
Issue. 4,
p.
857.
Soskov, I. N.
2013.
Effective properties of Marker's extensions.
Journal of Logic and Computation,
Vol. 23,
Issue. 6,
p.
1335.
Fokina, Ekaterina B.
Harizanov, Valentina
and
Melnikov, Alexander
2014.
Turing's Legacy.
p.
124.
Csima, Barbara F.
and
Knoll, Carolyn
2015.
Measuring complexities of classes of structures.
Annals of Pure and Applied Logic,
Vol. 166,
Issue. 12,
p.
1365.
2016.
Algebraic Computability and Enumeration Models.
p.
155.
Melnikov, Alexander G.
2017.
New Degree Spectra of Abelian Groups.
Notre Dame Journal of Formal Logic,
Vol. 58,
Issue. 4,
Montalbán, Antonio
2018.
Coding and Definability in Computable Structures.
Notre Dame Journal of Formal Logic,
Vol. 59,
Issue. 3,
Melnikov, A. G.
2021.
New Degree Spectra of Polish Spaces.
Siberian Mathematical Journal,
Vol. 62,
Issue. 5,
p.
882.
Bazhenov, Nikolay
and
Tsai, Hsing‐Chien
2022.
On the effective universality of mereological theories.
Mathematical Logic Quarterly,
Vol. 68,
Issue. 1,
p.
48.
Bazhenov, Nikolay
2023.
Computable Heyting Algebras with Distinguished Atoms and Coatoms.
Journal of Logic, Language and Information,
Vol. 32,
Issue. 1,
p.
3.
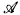 is a countable structure with finite signature, and d is a degree, we say that
is a countable structure with finite signature, and d is a degree, we say that 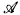 has αth-jump degreed if d is the least degree which is the αth jump of some degree c such there is an isomorphic copy of
has αth-jump degreed if d is the least degree which is the αth jump of some degree c such there is an isomorphic copy of 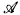 with universe ω in which the functions and relations have degree at most c. We show that every degree d ≥ 0(ω) is the ωth jump degree of a Boolean algebra, but that for n < ω no Boolean algebra has nth-jump degree d < 0(n). The former result follows easily from work of L. Feiner. The proof of the latter result uses the forcing methods of J. Knight together with an analysis of various equivalences between Boolean algebras based on a study of their Stone spaces. A byproduct of the proof is a method for constructing Stone spaces with various prescribed properties.
with universe ω in which the functions and relations have degree at most c. We show that every degree d ≥ 0(ω) is the ωth jump degree of a Boolean algebra, but that for n < ω no Boolean algebra has nth-jump degree d < 0(n). The former result follows easily from work of L. Feiner. The proof of the latter result uses the forcing methods of J. Knight together with an analysis of various equivalences between Boolean algebras based on a study of their Stone spaces. A byproduct of the proof is a method for constructing Stone spaces with various prescribed properties.