Published online by Cambridge University Press: 12 March 2014
This note answers a questions from [2] by showing that considered up to Borel reducibility, there are more essentially countable Borel equivalence relations than countable Borel equivalence relations. Namely:
Theorem 0.1. There is an essentially countable Borel equivalence relation E such that for no countable Borel equivalence relation F (on a standard Borel space) do we have
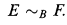
The proof of the result is short. It does however require an extensive rear guard campaign to extract from the techniques of [1] the following
Messy Fact 0.2. There are countable Borel equivalence relations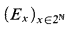 such that:
such that:
(i) eachExis defined on a standard Borel probability space (Xx, μx); each Ex is μx-invariant and μx-ergodic;
(ii) forx1 ≠ x2 and A μxι -conull, we haveExι/Anot Borel reducible toEx2;
(iii) if f: Xx → Xxis a measurable reduction ofExto itself then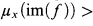
(iv)
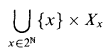
is a standard Borel space on which the projection function
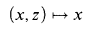
is Borel and the equivalence relation Ê given by
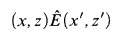
if and only ifx = x′ andzExz′ is Borel;
(V)
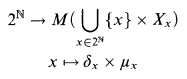
is Borel.
We first prove the theorem granted this messy fact. We then prove the fact.
(iv) and (v) are messy and unpleasant to state precisely, but are intended to express the idea that we have an effective parameterization of countable Borel equivalence relations by points in a standard Borel space. Examples along these lines appear already in the Adams-Kechris constructions; the new feature is (iii).
Simon Thomas has pointed out to me that in light of theorem 4.4 [5] the Gefter-Golodets examples of section 5 [5] also satisfy the conclusion of 0.2.