Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Leitgeb, Hannes
2007.
What Theories of Truth Should be Like (but Cannot be).
Philosophy Compass,
Vol. 2,
Issue. 2,
p.
276.
FEFERMAN, SOLOMON
2008.
AXIOMS FOR DETERMINATENESS AND TRUTH.
The Review of Symbolic Logic,
Vol. 1,
Issue. 2,
p.
204.
HALBACH, VOLKER
2009.
REDUCING COMPOSITIONAL TO DISQUOTATIONAL TRUTH.
The Review of Symbolic Logic,
Vol. 2,
Issue. 4,
p.
786.
Incurvati, L.
2009.
Does truth equal provability in the maximal theory?.
Analysis,
Vol. 69,
Issue. 2,
p.
233.
Horsten, L.
2009.
Levity.
Mind,
Vol. 118,
Issue. 471,
p.
555.
Welch, P. D.
2009.
Games for Truth.
The Bulletin of Symbolic Logic,
Vol. 15,
Issue. 4,
p.
410.
Fujimoto, Kentaro
2010.
Relative Truth Definability of Axiomatic Truth Theories.
The Bulletin of Symbolic Logic,
Vol. 16,
Issue. 3,
p.
305.
Leigh, Graham E.
2010.
S. Feferman. Reflecting on incompleteness. The Journal of Symbolic Logic, vol. 56 (1991), no. 1, pp. 1–49. -
W. N. Reinhardt. Some remarks on extending and interpreting theories with a partial predicate for truth. Journal of Philosophical Logic, vol. 15 (1986), no. 2, pp. 219–251. -
V. Halbach and L. Horsten. Axiomatizing Kripke’s theory of truth. The Journal of Symbolic Logic, vol. 71 (2006), no. 2, pp. 667–712
-
H. Friedman and M. Sheard. An axiomatic approach to self-referential truth.Annals of Pure and Applied Logic, vol. 33 (1987), no. 1, pp. 1–21. -
V. Halbach. A system of complete and consistent truth. Notre Dame Journal of Formal Logic, vol. 35 (1994), no. 3, pp. 311–327..
The Bulletin of Symbolic Logic,
Vol. 16,
Issue. 3,
p.
424.
WELCH, P. D.
2011.
TRUTH, LOGICAL VALIDITY AND DETERMINATENESS: A COMMENTARY ON FIELD’SSAVING TRUTH FROM PARADOX.
The Review of Symbolic Logic,
Vol. 4,
Issue. 3,
p.
348.
Ripley, David
2012.
Response to Heck.
Thought: A Journal of Philosophy,
Vol. 1,
Issue. 4,
p.
254.
HORSTEN, LEON
LEIGH, GRAHAM E.
LEITGEB, HANNES
and
WELCH, PHILIP
2012.
REVISION REVISITED.
The Review of Symbolic Logic,
Vol. 5,
Issue. 4,
p.
642.
Ripley, David
2012.
Response to Heck.
Thought: A Journal of Philosophy,
Vol. 1,
Issue. 4,
p.
254.
McGee, Vann
2013.
Book Reviews.
Studia Logica,
Vol. 101,
Issue. 3,
p.
641.
Leigh, G.E.
2013.
A proof-theoretic account of classical principles of truth.
Annals of Pure and Applied Logic,
Vol. 164,
Issue. 10,
p.
1009.
Cobreros, P.
Egre, P.
Ripley, D.
and
van Rooij, R.
2013.
Reaching Transparent Truth.
Mind,
Vol. 122,
Issue. 488,
p.
841.
Dean, Walter
and
Kurokawa, Hidenori
2014.
The Paradox of the Knower revisited.
Annals of Pure and Applied Logic,
Vol. 165,
Issue. 1,
p.
199.
Scharp, Kevin
2014.
Truth, Revenge, and Internalizability.
Erkenntnis,
Vol. 79,
Issue. S3,
p.
597.
FISCHER, MARTIN
HALBACH, VOLKER
KRIENER, JÖNNE
and
STERN, JOHANNES
2015.
AXIOMATIZING SEMANTIC THEORIES OF TRUTH?.
The Review of Symbolic Logic,
Vol. 8,
Issue. 2,
p.
257.
Halbach, Volker
and
Horsten, Leon
2015.
Unifying the Philosophy of Truth.
Vol. 36,
Issue. ,
p.
263.
Terzian, Giulia
2015.
Norms of Truth and Logical Revision.
Topoi,
Vol. 34,
Issue. 1,
p.
15.
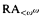 ramified analysis or a system of Tarskian ramified truth up to ωω. Thus any such axiomatization is much weaker than Feferman's axiomatization KF in classical logic, which is equivalent to the system
ramified analysis or a system of Tarskian ramified truth up to ωω. Thus any such axiomatization is much weaker than Feferman's axiomatization KF in classical logic, which is equivalent to the system 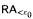 of ramified analysis up to ε0.
of ramified analysis up to ε0.
