No CrossRef data available.
Article contents
ASYMPTOTIC ANALYSIS OF SKOLEM’S EXPONENTIAL FUNCTIONS
Published online by Cambridge University Press: 04 September 2020
Abstract
Skolem (1956) studied the germs at infinity of the smallest class of real valued functions on the positive real line containing the constant 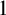 $1$, the identity function
$1$, the identity function 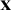 ${\mathbf {x}}$, and such that whenever f and g are in the set,
${\mathbf {x}}$, and such that whenever f and g are in the set, 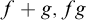 $f+g,fg$ and
$f+g,fg$ and 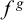 $f^g$ are in the set. This set of germs is well ordered and Skolem conjectured that its order type is epsilon-zero. Van den Dries and Levitz (1984) computed the order type of the fragment below
$f^g$ are in the set. This set of germs is well ordered and Skolem conjectured that its order type is epsilon-zero. Van den Dries and Levitz (1984) computed the order type of the fragment below 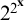 $2^{2^{\mathbf {x}}}$. Here we prove that the set of asymptotic classes within any Archimedean class of Skolem functions has order type
$2^{2^{\mathbf {x}}}$. Here we prove that the set of asymptotic classes within any Archimedean class of Skolem functions has order type 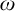 $\omega $. As a consequence we obtain, for each positive integer n, an upper bound for the fragment below
$\omega $. As a consequence we obtain, for each positive integer n, an upper bound for the fragment below 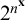 $2^{n^{\mathbf {x}}}$. We deduce an epsilon-zero upper bound for the fragment below
$2^{n^{\mathbf {x}}}$. We deduce an epsilon-zero upper bound for the fragment below 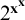 $2^{{\mathbf {x}}^{\mathbf {x}}}$, improving the previous epsilon-omega bound by Levitz (1978). A novel feature of our approach is the use of Conway’s surreal number for asymptotic calculations.
$2^{{\mathbf {x}}^{\mathbf {x}}}$, improving the previous epsilon-omega bound by Levitz (1978). A novel feature of our approach is the use of Conway’s surreal number for asymptotic calculations.
MSC classification
Information
- Type
- Article
- Information
- Copyright
- © The Author(s), 2020. Published by Cambridge University Press on behalf of The Association for Symbolic Logic


