Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Gao, Su
and
Zhang, Yi
2008.
Definable sets of generators in maximal cofinitary groups.
Advances in Mathematics,
Vol. 217,
Issue. 2,
p.
814.
Friedman, Sy-David
and
Zdomskyy, Lyubomyr
2010.
Projective mad families.
Annals of Pure and Applied Logic,
Vol. 161,
Issue. 12,
p.
1581.
Fischer, Vera
Friedman, Sy David
and
Khomskii, Yurii
2013.
Co-analytic mad families and definable wellorders.
Archive for Mathematical Logic,
Vol. 52,
Issue. 7-8,
p.
809.
Hrušák, Michael
2014.
Recent Progress in General Topology III.
p.
601.
Horowitz, Haim
and
Shelah, Saharon
2024.
A Borel maximal eventually different family.
Annals of Pure and Applied Logic,
Vol. 175,
Issue. 1,
p.
103334.

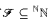 is an analytic family of pairwise eventually different functions then the following strong maximality condition fails: For any countable
is an analytic family of pairwise eventually different functions then the following strong maximality condition fails: For any countable 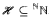 , no member of which is covered by finitely many functions from
, no member of which is covered by finitely many functions from 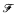 , there is
, there is 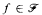 such that for all
such that for all 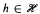 there are infinitely many integers
there are infinitely many integers 