Published online by Cambridge University Press: 12 March 2014
Let p be a fixed prime integer, other than 2, Qp the field of p-adic numbers, and Ωp the completion of the algebraic closure of Qp. Let Rp be the ring of entire functions in one variable t over Ωp; that is, Rp is the ring of functions f: Ωp → Qp such that f(t) is given by a power series around 0, of infinite radius of convergence:
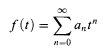
and 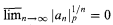 where ∣a∣p is the p-adic norm of a in Ωp. We prove:
where ∣a∣p is the p-adic norm of a in Ωp. We prove:
Theorem A. The positive existential theory of Rp in the language L = {0, 1, t, +, ·} is undecidable.
Theorem A gives a negative answer to the analogue of Hilbert's tenth problem for Rp in the language L. Related results include those of [2] where it is shown that the first-order theory of entire functions on the complex plane is undecidable and the similar result for analytic functions on the open unit disk (this is due to Denef and Gromov, communicated to us by Cherlin and is as of now unpublished).
It would be desirable to have a similar result in the language which, instead of the variable t, has a predicate for the transcendental (that is, nonconstant) elements of Rp. A related problem is the similar problem for meromorphic functions on the real or p-adic plane or on the unit open or closed disk. These problems seem for the moment rather hard in view of the fact that the analogue of Hilbert's Tenth Problem for the field of rational functions over the complex numbers (or any algebraically closed field of characteristic zero) is an open problem.