Article contents
Actions by the classical Banach spaces
Published online by Cambridge University Press: 12 March 2014
Extract
The study of continuous group actions is ubiquitous in mathematics, and perhaps the most general kinds of actions for which we can hope to prove theorems in just ZFC are those where a Polish group acts on a Polish space.
For this general class we can find works such as [29] that build on ideas from ergodic theory and examine actions of locally compact groups in both the measure theoretic and topological contexts. On the other hand a text in model theory, such as [12], will typically consider issues bearing on the actions by the symmetric group of all permutations of the integers. More generally [1] shows that the orbit equivalence relations induced by closed subgroups of the infinite symmetric group can be reduced to the isomorphism relation on corresponding classes of countable models.
This paper considers a third category formed by the continuous actions of separable Banach spaces on Polish spaces. These examples cannot be subsumed under the two earlier headings, and it is known from [10] that the Borel cardinalities of the quotient spaces that arise from such actions are incomparable with the equivalence relations induced by the symmetric group or any locally compact Polish group action.
One of the first things to be addressed concerns the complexity of these equivalence relations. This question for 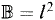 appears in [1].
appears in [1].
Information
- Type
- Research Article
- Information
- Copyright
- Copyright © Association for Symbolic Logic 2000
References
REFERENCES
- 11
- Cited by

