No CrossRef data available.
Published online by Cambridge University Press: 21 December 2018
Previous results about n-grids with acceptable colorings are extended here to n-indexed hyperspaces, which are structures 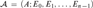 ${\cal A} = \left( {A;{E_0},{E_1}, \ldots ,{E_{n - 1}}} \right)$, where each
${\cal A} = \left( {A;{E_0},{E_1}, \ldots ,{E_{n - 1}}} \right)$, where each  ${E_i}$ is an equivalence relation on A.
${E_i}$ is an equivalence relation on A.