Article contents
TOPOLOGICAL CELL DECOMPOSITION AND DIMENSION THEORY IN P-MINIMAL FIELDS
Published online by Cambridge University Press: 21 March 2017
Abstract
This paper addresses some questions about dimension theory for P-minimal structures. We show that, for any definable set A, the dimension of 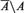 $\bar A\backslash A$ is strictly smaller than the dimension of A itself, and that A has a decomposition into definable, pure-dimensional components. This is then used to show that the intersection of finitely many definable dense subsets of A is still dense in A. As an application, we obtain that any definable function
$\bar A\backslash A$ is strictly smaller than the dimension of A itself, and that A has a decomposition into definable, pure-dimensional components. This is then used to show that the intersection of finitely many definable dense subsets of A is still dense in A. As an application, we obtain that any definable function 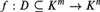 $f:D \subseteq {K^m} \to {K^n}$ is continuous on a dense, relatively open subset of its domain D, thereby answering a question that was originally posed by Haskell and Macpherson.
$f:D \subseteq {K^m} \to {K^n}$ is continuous on a dense, relatively open subset of its domain D, thereby answering a question that was originally posed by Haskell and Macpherson.
In order to obtain these results, we show that P-minimal structures admit a type of cell decomposition, using a topological notion of cells inspired by real algebraic geometry.
Information
- Type
- Articles
- Information
- Copyright
- Copyright © The Association for Symbolic Logic 2017
References
REFERENCES
- 11
- Cited by

