Article contents
Théories d'algèbres de Boole munies d'idéaux distingués. II
Published online by Cambridge University Press: 12 March 2014
Extract
La première partie de cet article ([10], que nous désignerons par (I) dans la suite) était consacrée à la théorie élémentaire TX des algèbres de Boole munies d'idéaux distingués indéxés dans un ensemble X. On a vu que les idéaux définissables dans un modèle 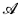 de Tx forment la sous-algèbre engendrée par les idéaux distingués de l'algèbre de Heyting des idéaux de
de Tx forment la sous-algèbre engendrée par les idéaux distingués de l'algèbre de Heyting des idéaux de 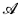 munie de l'opérateur sa défini par sa(K) = {a: a/K est sans atome}, et que la théorie de
munie de l'opérateur sa défini par sa(K) = {a: a/K est sans atome}, et que la théorie de 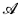 peut être caractérisée par la structure
peut être caractérisée par la structure 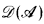 composée de l'algèbre de Heyting des idéaux définissables munie de l'opérateur sa et des idéaux distingués, et par l'application qui à tout K de
composée de l'algèbre de Heyting des idéaux définissables munie de l'opérateur sa et des idéaux distingués, et par l'application qui à tout K de 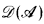 fait correspondre le nombre d'atomes de
fait correspondre le nombre d'atomes de 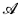 /K, pris dans N ⋃ {∞}.
/K, pris dans N ⋃ {∞}.
Nous montrons maintenant que les structures 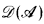 possibles peuvent être définies de façon axiomatique en introduisant une classe équationnelle d'algèbres de Heyting munies d'une opération unaire, dites sa-algèbres de Heyting (en abrégé sa-AH), et en prouvant que cette classe est constituée des algèbres pouvant être plongées dans l'algèbre de Heyting des idéaux d'une algèbre de Boole, munie de l'opérateur sa. Ainsi les
possibles peuvent être définies de façon axiomatique en introduisant une classe équationnelle d'algèbres de Heyting munies d'une opération unaire, dites sa-algèbres de Heyting (en abrégé sa-AH), et en prouvant que cette classe est constituée des algèbres pouvant être plongées dans l'algèbre de Heyting des idéaux d'une algèbre de Boole, munie de l'opérateur sa. Ainsi les 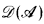 sont, à isomorphisme près, les sa-AH engendrées par des éléments distingués indéxés dans X; on en déduit une classification des extensions complètes de Tx en montrant que les applications qui peuvent être associées à une structure de la forme
sont, à isomorphisme près, les sa-AH engendrées par des éléments distingués indéxés dans X; on en déduit une classification des extensions complètes de Tx en montrant que les applications qui peuvent être associées à une structure de la forme 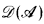 pour caractériser la théorie d'un modèle sont déterminées par leur restriction à une partie M(
pour caractériser la théorie d'un modèle sont déterminées par leur restriction à une partie M(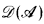 ) définie uniformément, sur laquelle elles prennent des valeurs dans (N − {0}) ⋃ {∞}, et que réciproquement toute application de M(
) définie uniformément, sur laquelle elles prennent des valeurs dans (N − {0}) ⋃ {∞}, et que réciproquement toute application de M(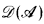 ) dans (N − {0}) ⋃ {∞} est une telle restriction.
) dans (N − {0}) ⋃ {∞} est une telle restriction.
Information
- Type
- Research Article
- Information
- Copyright
- Copyright © Association for Symbolic Logic 1990
References
RÉFÉRENCES
- 7
- Cited by

