Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Jackson, Steve
2010.
Handbook of Set Theory.
p.
1753.
Sargsyan, Grigor
2019.
An inner model theoretic proof of Becker’s theorem.
Archive for Mathematical Logic,
Vol. 58,
Issue. 7-8,
p.
999.

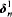 are supercompact through their supremum
are supercompact through their supremum 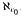 and a ways beyond.
and a ways beyond.