Article contents
The structure of algebraically and existentially closed Stone and double Stone algebras
Published online by Cambridge University Press: 12 March 2014
Extract
In this paper we study the varieties of Stone algebras (S, ∧, ∨, *, 0, 1) and double Stone algebras (D, ∧, ∨, *, +, 0, 1). Our primary interest is to give a structural description of the algebraically and existentially closed members of both classes. Our technique is an application of the natural dualities of Davey [6] and Clark and Krauss [5]. This approach gives a description of the desired models as the algebras of all continuous structure-preserving maps from certain structured Boolean spaces into the generating algebra for the variety. In each case the resulting description can be converted in a natural way into a finite ∀∃-axiomatization for these models. For Stone algebras these axioms appeared earlier in Schmid [20], [21] and in Schmitt [22].
Since both cases we consider satisfy the amalgamation property, the existentially closed members form a model companion for the variety which is also its model completion. Moreover, it is also ℵ0 categorical and its countably infinite member is the unique countable homogeneous universal model for the variety. In the case of Stone algebras, explicit constructions for this model appear in Schmitt [22] and Weispfenning [23]. We give here an explicit construction for double Stone algebras of S. Hayes.
This work was motivated by a problem of Stanley Burris. In [4] Burris and Werner superseded many previous results by showing that for any finite algebra A, the universal Horn class ISP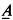 has a model companion. Weispfenning [24], [25] discovered that this model companion is always ℵ0 categorical and has a primitive recursive ∀∃-axiomatization. In spite of these very general theorems, there are few instances in which a structural description of the (any!) existentially closed members of ISP
has a model companion. Weispfenning [24], [25] discovered that this model companion is always ℵ0 categorical and has a primitive recursive ∀∃-axiomatization. In spite of these very general theorems, there are few instances in which a structural description of the (any!) existentially closed members of ISP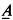 is available. Burris and Werner [4] solve this problem in a special setting.
is available. Burris and Werner [4] solve this problem in a special setting.
Information
- Type
- Research Article
- Information
- Copyright
- Copyright © Association for Symbolic Logic 1989
References
REFERENCES
- 5
- Cited by

