Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Liu, Kecheng
and
Shelah, Saharon
1997.
Cofinalities of elementary substructures of structures on ℵω.
Israel Journal of Mathematics,
Vol. 99,
Issue. 1,
p.
189.
Foreman, Matthew
and
Magidor, Menachem
2001.
Mutually stationary sequences of sets and the non-saturation of the non-stationary ideal on Pϰ(λ).
Acta Mathematica,
Vol. 186,
Issue. 2,
p.
271.
Koepke, Peter
2006.
Forcing a mutual stationarity property in cofinality 𝜔₁.
Proceedings of the American Mathematical Society,
Vol. 135,
Issue. 5,
p.
1523.
Adolf, Dominik
Cox, Sean
and
Welch, Philip
2018.
Lower consistency bounds for mutual stationarity with divergent uncountable cofinalities.
Israel Journal of Mathematics,
Vol. 228,
Issue. 1,
p.
1.

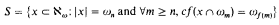
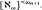
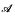 on ℵ
on ℵ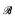 ≺
≺ 