Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Eisworth, Todd
2014.
On idealized versions of Pr1(μ +, μ +, μ +, cf(μ)).
Archive for Mathematical Logic,
Vol. 53,
Issue. 7-8,
p.
809.

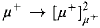 holds for a singular cardinal
holds for a singular cardinal 