Article contents
Regressive partitions and Borel diagonalization
Published online by Cambridge University Press: 12 March 2014
Extract
Several rather concrete propositions about Borel measurable functions of several variables on the Hilbert cube (countable sequences of reals in the unit interval) were formulated by Harvey Friedman [F1] and correlated with strong set-theoretic hypotheses. Most notably, he established that a “Borel diagonalization” proposition P is equivalent to: for any a ⊆ co and n ⊆ ω there is an ω-model of ZFC + ∃κ(κ is n-Mahlo) containing a. In later work (see the expository Stanley [St] and Friedman [F2]), Friedman was to carry his investigations further into propositions about spaces of groups and the like, and finite propositions. He discovered and analyzed mathematical propositions which turned out to have remarkably strong consistency strength in terms of large cardinal hypotheses in set theory.
In this paper, we refine and extend Friedman's work on the Borel diagonalization proposition P. First, we provide more combinatorics about regressive partitions and n-Mahlo cardinals and extend the approach to the context of the Erdös cardinals 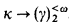 In passing, a combinatorial proof of a well-known result of Silver about these cardinals is given. Incorporating this work and sharpening Friedman's proof, we then show that there is a level-by-level analysis of P which provides for each n ⊆ ω a proposition almost equivalent to: for any a ⊆ co there is an ω-model of ZFC + ∃κ(κ is n-Mahlo) containing a. Finally, we use the combinatorics to bracket a natural generalization Sω of P between two large cardinal hypotheses.
In passing, a combinatorial proof of a well-known result of Silver about these cardinals is given. Incorporating this work and sharpening Friedman's proof, we then show that there is a level-by-level analysis of P which provides for each n ⊆ ω a proposition almost equivalent to: for any a ⊆ co there is an ω-model of ZFC + ∃κ(κ is n-Mahlo) containing a. Finally, we use the combinatorics to bracket a natural generalization Sω of P between two large cardinal hypotheses.
Information
- Type
- Research Article
- Information
- Copyright
- Copyright © Association for Symbolic Logic 1989
References
REFERENCES
- 1
- Cited by

