Hostname: page-component-cb9f654ff-qc88w Total loading time: 0 Render date: 2025-08-17T19:25:23.579Z Has data issue: false hasContentIssue false
  • English
  • Français

REFLECTION RANKS AND ORDINAL ANALYSIS

Part of: Proof theory and constructive mathematics

Published online by Cambridge University Press:  10 July 2020

FEDOR PAKHOMOV  and
JAMES WALSH
FEDOR PAKHOMOV
Affiliation:
STEKLOV MATHEMATICAL INSTITUTE OF RUSSIAN ACADEMY OF SCIENCES 8, GUBKINA STREET, MOSCOW 119991, RUSSIAN FEDERATION and INSTITUTE OF MATHEMATICS OF THE CZECH ACADEMY OF SCIENCES, ŽITNÁ 25, 115 67 PRAHA 1, CZECH REPUBLIC E-mail: pakhfn@mi-ras.ru E-mail: pakhomov@math.cas.cz
JAMES WALSH
Affiliation:
DEPARTMENT OF PHILOSOPHY CORNELL UNIVERSITY ITHACA, NY 14853, USA E-mail: jameswalsh@cornell.edu
Get access Rights & Permissions [Opens in a new window]

Abstract

It is well-known that natural axiomatic theories are well-ordered by consistency strength. However, it is possible to construct descending chains of artificial theories with respect to consistency strength. We provide an explanation of this well-orderedness phenomenon by studying a coarsening of the consistency strength order, namely, the 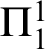$\Pi ^1_1$ reflection strength order. We prove that there are no descending sequences of 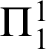$\Pi ^1_1$ sound extensions of $\mathsf {ACA}_0$ in this ordering. Accordingly, we can attach a rank in this order, which we call reflection rank, to any 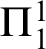$\Pi ^1_1$ sound extension of $\mathsf {ACA}_0$. We prove that for any 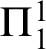$\Pi ^1_1$ sound theory T extending $\mathsf {ACA}_0^+$, the reflection rank of T equals the 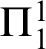$\Pi ^1_1$ proof-theoretic ordinal of T. We also prove that the 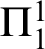$\Pi ^1_1$ proof-theoretic ordinal of 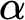$\alpha $ iterated 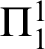$\Pi ^1_1$ reflection is 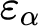$\varepsilon _\alpha $. Finally, we use our results to provide straightforward well-foundedness proofs of ordinal notation systems based on reflection principles.

Keywords

reflection principlesordinal analysissecond-order arithmeticfirst-order arithmetic

MSC classification

Primary: 03F15: Recursive ordinals and ordinal notations
Secondary: 03F35: Second- and higher-order arithmetic and fragments

Information

Type
Article
Information
The Journal of Symbolic Logic , Volume 86 , Issue 4 , December 2021 , pp. 1350 - 1384
Check for updates
Copyright
© Association for Symbolic Logic 2020

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

Beklemishev, L., Iterated local reflection versus iterated consistency. Annals of Pure and Applied Logic, vol. 75 (1995), no. 1–2, pp. 25–48.10.1016/0168-0072(95)00007-4CrossRefGoogle Scholar
Beklemishev, L., Proof-theoretic analysis by iterated reflection. Archive for Mathematical Logic, vol. 42 (2003), no. 6, pp. 515–552.10.1007/s00153-002-0158-7CrossRefGoogle Scholar
Beklemishev, L., Provability algebras and proof-theoretic ordinals, I. Annals of Pure and Applied Logic, vol. 128 (2004), no. 1–3, pp. 103–123.10.1016/j.apal.2003.11.030CrossRefGoogle Scholar
Beklemishev, L., Reflection principles and provability algebras in formal arithmetic. Russian Mathematical Surveys, vol. 60 (2005), no. 2, p. 197.CrossRefGoogle Scholar
Beklemishev, L., Veblen hierarchy in the context of provability algebras, Logic, Methodology and Philosophy of Science, Proceedings of the Twelfth International Congress (Hájek, P., Valdés-Villanueva, L., and Westerståhl, D., editors), Kings College Publications, London, 2005, pp. 65–78. Preprint: Logic Group Preprint Series 232, Utrecht University, June 2004.Google Scholar
Beklemishev, L., Calibrating provability logic: From modal logic to reflection calculus. Advances in Modal Logic, vol. 9 (2012), pp. 89–94.Google Scholar
Beklemishev, L., Positive provability logic for uniform reflection principles. Annals of Pure and Applied Logic, vol. 165 (2014), no. 1, pp. 82–105.10.1016/j.apal.2013.07.006CrossRefGoogle Scholar
Beklemishev, L., Reflection calculus and conservativity spectra. Russian Mathematical Surveys, vol. 73 (2018), no. 4, pp. 569–613.10.1070/RM9843CrossRefGoogle Scholar
Beklemishev, L. and Pakhomov, F., Reflection algebras and conservation results for theories of iterated truth, 2019. arXiv:1908.10302.Google Scholar
Dashkov, E., On the positive fragment of the polymodal provability logic GLP . Mathematical Notes, vol. 91 (2012), no. 3–4, pp. 318–333.10.1134/S0001434612030029CrossRefGoogle Scholar
Enayat, A. and Pakhomov, F., Truth, disjunction, and induction. Archive for Mathematical Logic, vol. 58 (2019), no. 5, pp. 753–766.10.1007/s00153-018-0657-9CrossRefGoogle Scholar
Fernández-Duque, D., Worms and spiders: Reflection calculi and ordinal notation systems, 2016. arXiv:1605.08867.Google Scholar
Friedman, H., Uniformly defined descending sequences of degrees, this Journal, vol. 41 (1976), no. 2, pp. 363–367.Google Scholar
Frittaion, E., Uniform reflection in second order arithmetic, 2019. Available at https://drive.google.com/file/d/19-25_Gr5wGE6beQD5ho_k52slivagTjU/view.Google Scholar
Hájek, P. and Pudlák, P., Metamathematics of First-Order Arithmetic, Cambridge University Press, Cambridge, 2017.Google Scholar
Kreisel, G. and Lévy, A., Reflection principles and their use for establishing the complexity of axiomatic systems. Mathematical Logic Quarterly, vol. 14 (1968), no. 7–12, pp. 97–142.CrossRefGoogle Scholar
Lindström, P., Aspects of Incompleteness, Cambridge University Press, Cambridge, 2017.Google Scholar
Lutz, P. and Walsh, J., Incompleteness and jump hierarchies, 2019. arXiv:1909.10603.Google Scholar
Pakhomov, F. and Walsh, J., Reflection ranks and ordinal analysis, 2018. arXiv:1805.02095v1.10.1017/jsl.2020.9CrossRefGoogle Scholar
Pohlers, W., Proof Theory: The First Step into Impredicativity, Springer Science, New York, 2008.Google Scholar
Rathjen, M., The realm of ordinal analysis, Sets and Proofs (Cooper, S. B. and Truss, J. K., editors), Cambridge University Press, Cambridge, 1999, pp. 219–279.10.1017/CBO9781107325944.011CrossRefGoogle Scholar
Schmerl, U. R., A fine structure generated by reflection formulas over primitive recursive arithmetic. Studies in Logic and the Foundations of Mathematics, vol. 97 (1979), pp. 335–350.10.1016/S0049-237X(08)71633-1CrossRefGoogle Scholar
Schmerl, U. R., Iterated reflection principles and the  $\omega$ -rule, this Journal, vol. 47 (1982), no. 4, pp. 721–733.Google Scholar
Simpson, S. G., Subsystems of Second Order Arithmetic, Cambridge University Press, Cambridge, 2009.10.1017/CBO9780511581007CrossRefGoogle Scholar
Simpson, S. G. and Smith, R. L., Factorization of polynomials and $\varSigma$ 10 induction. Annals of Pure and Applied Logic, vol. 31 (1986), no. 2, pp. 289–306.10.1016/0168-0072(86)90074-6CrossRefGoogle Scholar
Smorynski, C., Self-Reference and Modal Logic, Springer Science & Business Media, New York, 2012.Google Scholar
Steel, J., Descending sequences of degrees, this Journal, vol. 40 (1975), no. 1, pp. 59–61.Google Scholar