No CrossRef data available.
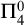 $\Pi ^0_4$ CONSERVATION OF THE ORDERED VARIABLE WORD THEOREM
$\Pi ^0_4$ CONSERVATION OF THE ORDERED VARIABLE WORD THEOREMPublished online by Cambridge University Press: 27 January 2025
A left-variable word over an alphabet A is a word over 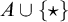 $A \cup \{\star \}$ whose first letter is the distinguished symbol
$A \cup \{\star \}$ whose first letter is the distinguished symbol  $\star $ standing for a placeholder. The ordered variable word theorem (
$\star $ standing for a placeholder. The ordered variable word theorem (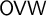 $\mathsf {OVW}$), also known as Carlson–Simpson’s theorem, is a tree partition theorem, stating that for every finite alphabet A and every finite coloring of the words over A, there exists a word
$\mathsf {OVW}$), also known as Carlson–Simpson’s theorem, is a tree partition theorem, stating that for every finite alphabet A and every finite coloring of the words over A, there exists a word 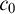 $c_0$ and an infinite sequence of left-variable words
$c_0$ and an infinite sequence of left-variable words 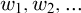 $w_1, w_2, \dots $ such that
$w_1, w_2, \dots $ such that 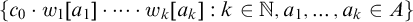 $\{ c_0 \cdot w_1[a_1] \cdot \dots \cdot w_k[a_k] : k \in \mathbb {N}, a_1, \dots , a_k \in A \}$ is monochromatic.
$\{ c_0 \cdot w_1[a_1] \cdot \dots \cdot w_k[a_k] : k \in \mathbb {N}, a_1, \dots , a_k \in A \}$ is monochromatic.
In this article, we prove that 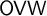 $\mathsf {OVW}$ is
$\mathsf {OVW}$ is 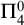 $\Pi ^0_4$-conservative over
$\Pi ^0_4$-conservative over 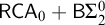 $\mathsf {RCA}_0 + \mathsf {B}\Sigma ^0_2$. This implies in particular that
$\mathsf {RCA}_0 + \mathsf {B}\Sigma ^0_2$. This implies in particular that 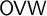 $\mathsf {OVW}$ does not imply
$\mathsf {OVW}$ does not imply  $\mathsf {ACA}_0$ over
$\mathsf {ACA}_0$ over  $\mathsf {RCA}_0$. This is the first principle for which the only known separation from
$\mathsf {RCA}_0$. This is the first principle for which the only known separation from  $\mathsf {ACA}_0$ involves non-standard models.
$\mathsf {ACA}_0$ involves non-standard models.