Article contents
On the ranked points of a Π10 set
Published online by Cambridge University Press: 12 March 2014
Abstract
This paper continues joint work of the authors with P. Clote, R. Soare and S. Wainer (Annals of Pure and Applied Logic, vol. 31 (1986), pp. 145–163). An element x of the Cantor space 2ω is said have rank α in the closed set P if x is in Dα(P)/Dα + 1(P), where Dα is the iterated Cantor-Bendixson derivative. The rank of x is defined to be the least α such that x has rank a in some 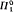 set. The main result of the five-author paper is that for any recursive ordinal λ + n (where λ is a limit and n is finite), there is a point with rank λ + n which is Turing equivalent to O(λ + 2n) All ranked points constructed in that paper are
set. The main result of the five-author paper is that for any recursive ordinal λ + n (where λ is a limit and n is finite), there is a point with rank λ + n which is Turing equivalent to O(λ + 2n) All ranked points constructed in that paper are 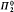 singletons. We now construct a ranked point which is not a
singletons. We now construct a ranked point which is not a 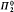 singleton. In the previous paper the points of high rank were also of high hyperarithmetic degree. We now construct
singleton. In the previous paper the points of high rank were also of high hyperarithmetic degree. We now construct 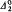 points with arbitrarily high rank. We also show that every nonrecursive RE point is Turing equivalent to an RE point of rank one and that every nonrecursive
points with arbitrarily high rank. We also show that every nonrecursive RE point is Turing equivalent to an RE point of rank one and that every nonrecursive 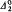 point is Turing equivalent to a hyperimmune point of rank one. We relate Clote's notion of the height of a
point is Turing equivalent to a hyperimmune point of rank one. We relate Clote's notion of the height of a 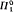 singleton in the Baire space with the notion of rank. Finally, we show that every hyperimmune point x is Turing equivalent to a point which is not ranked.
singleton in the Baire space with the notion of rank. Finally, we show that every hyperimmune point x is Turing equivalent to a point which is not ranked.
Information
- Type
- Research Article
- Information
- Copyright
- Copyright © Association for Symbolic Logic 1989
References
REFERENCES
- 8
- Cited by

