Article contents
On partitions of the real line into compact sets
Published online by Cambridge University Press: 12 March 2014
Extract
The problem mentioned in the title has already been investigated by J. Baumgartner, J. Stern, A. Miller and many others (see [2] and [5]). We prove here some generalizations of theorems of Miller and Stern from [2] and [5]. We use standard set-theoretical notation. Let
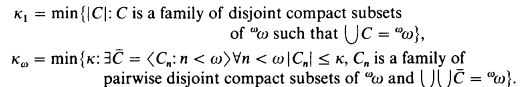
One can check that in the above definition we can replace “compact subset of ωω” by “closed nowhere dense subset of ω2” or “Fσ and meager subset of ω2” (as any Fσ subset of ω2 can be presented as a disjoint countable union of compact sets).
For functions f, g ϵ ωω we define f ≼ g if for all but finitely many n ϵ ω we have f(n) ≤ g(n). Let 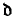 denote the least cardinality of a family A ⊆ ωω such that for any f ϵ ωω there is g ϵ A for which f ≼ g. It is easy to see that
denote the least cardinality of a family A ⊆ ωω such that for any f ϵ ωω there is g ϵ A for which f ≼ g. It is easy to see that 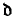 ≤ κω ≤ κ1. If f ϵ ωω then let ≼(f) = {h ϵωω: h ≼ f}.
≤ κω ≤ κ1. If f ϵ ωω then let ≼(f) = {h ϵωω: h ≼ f}.
We find an axiom which implies 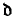 = ω1 → κ1 = ω1, and which can be preserved by any ccc notion of forcing of “small cardinality”. We construct also in a generic model many partitions of ωω into compact sets preserved not only by any random real extension, but also by Sacks' notion of forcing. This shows that from some point of view Miller's modification of Sacks' forcing (from [2]) is the “minimal” one able to destroy a partition of ωω into compact sets.
= ω1 → κ1 = ω1, and which can be preserved by any ccc notion of forcing of “small cardinality”. We construct also in a generic model many partitions of ωω into compact sets preserved not only by any random real extension, but also by Sacks' notion of forcing. This shows that from some point of view Miller's modification of Sacks' forcing (from [2]) is the “minimal” one able to destroy a partition of ωω into compact sets.
Information
- Type
- Research Article
- Information
- Copyright
- Copyright © Association for Symbolic Logic 1987
References
REFERENCES
- 5
- Cited by

