Published online by Cambridge University Press: 21 December 2018
Let 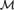 ${\cal M}$ be ternary, homogeneous and simple. We prove that if
${\cal M}$ be ternary, homogeneous and simple. We prove that if 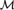 ${\cal M}$ is finitely constrained, then it is supersimple with finite SU-rank and dependence is k-trivial for some k < ω and for finite sets of real elements. Now suppose that, in addition,
${\cal M}$ is finitely constrained, then it is supersimple with finite SU-rank and dependence is k-trivial for some k < ω and for finite sets of real elements. Now suppose that, in addition, 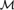 ${\cal M}$ is supersimple with SU-rank 1. If
${\cal M}$ is supersimple with SU-rank 1. If 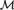 ${\cal M}$ is finitely constrained then algebraic closure in
${\cal M}$ is finitely constrained then algebraic closure in 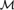 ${\cal M}$ is trivial. We also find connections between the nature of the constraints of
${\cal M}$ is trivial. We also find connections between the nature of the constraints of 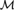 ${\cal M}$, the nature of the amalgamations allowed by the age of
${\cal M}$, the nature of the amalgamations allowed by the age of 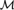 ${\cal M}$, and the nature of definable equivalence relations. A key method of proof is to “extract” constraints (of
${\cal M}$, and the nature of definable equivalence relations. A key method of proof is to “extract” constraints (of 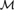 ${\cal M}$) from instances of dividing and from definable equivalence relations. Finally, we give new examples, including an uncountable family, of ternary homogeneous supersimple structures of SU-rank 1.
${\cal M}$) from instances of dividing and from definable equivalence relations. Finally, we give new examples, including an uncountable family, of ternary homogeneous supersimple structures of SU-rank 1.