Article contents
On characterizing Spector classes
Published online by Cambridge University Press: 12 March 2014
Extract
We study in this paper characterizations of various interesting classes of relations arising in recursion theory. We first determine which Spector classes on the structure of arithmetic arise from recursion in normal type 2 objects, giving a partial answer to a problem raised by Moschovakis [8], where the notion of Spector class was first essentially introduced. Our result here was independently discovered by S. G. Simpson (see [3]). We conclude our study of Spector classes by examining two simple relations between them and a natural hierarchy to which they give rise.
The second part of our paper is concerned with finding structural characterizations of classes of relations on the reals in the spirit of Moschovakis [7]. Our main result provides a single abstract characterization for the class of 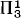 relations on the reals and the 2-envelope of 3E, the first one being valid if projective determinacy is true, the second if V = L is true.
relations on the reals and the 2-envelope of 3E, the first one being valid if projective determinacy is true, the second if V = L is true.
Information
- Type
- Research Article
- Information
- Copyright
- Copyright © Association for Symbolic Logic 1975
References
REFERENCES
- 6
- Cited by

