Article contents
On Π 1-automorphisms of recursive linear orders
Published online by Cambridge University Press: 12 March 2014
Extract
If σ is the order type of a recursive linear order which has a nontrivial automorphism, we let  denote the least complexity in the arithmetical hierarchy such that every recursive order of type σ has a nontrivial automorphism of complexity
denote the least complexity in the arithmetical hierarchy such that every recursive order of type σ has a nontrivial automorphism of complexity  . In Chapter 16 of his book Linear orderings [R], Rosenstein discussed the problem of determining
. In Chapter 16 of his book Linear orderings [R], Rosenstein discussed the problem of determining  for certain order types σ. For example Rosenstein proved that
for certain order types σ. For example Rosenstein proved that 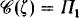 , where ζ is the order type of the integers, by constructing a recursive linear order of type ζ which has no nontrivial Σ 1-automorphism and showing that every recursive linear order of type ζ has a nontrivial Π 1-automorphism. Rosenstein also considered linear orders of order type 2 · η, where 2 is the order type of a two-element chain and η is the order type of the rational numbers. It is easily seen that any recursive linear order of type 2 · η has a nontrivial ⊿ 2-automorphism; he showed that there is a recursive linear order of type 2 · η that has no nontrivial Σ 1-automorphism. This left the question, posed in [R] and also by Lerman and Rosenstein in [LR], of whether
, where ζ is the order type of the integers, by constructing a recursive linear order of type ζ which has no nontrivial Σ 1-automorphism and showing that every recursive linear order of type ζ has a nontrivial Π 1-automorphism. Rosenstein also considered linear orders of order type 2 · η, where 2 is the order type of a two-element chain and η is the order type of the rational numbers. It is easily seen that any recursive linear order of type 2 · η has a nontrivial ⊿ 2-automorphism; he showed that there is a recursive linear order of type 2 · η that has no nontrivial Σ 1-automorphism. This left the question, posed in [R] and also by Lerman and Rosenstein in [LR], of whether  or ⊿ 2. The main result of this article is that
or ⊿ 2. The main result of this article is that  :
:
Information
- Type
- Research Article
- Information
- Copyright
- Copyright © Association for Symbolic Logic 1987
Footnotes
The author was supported in part by NSF grant IPS-80110451, ONR grant N00014-85K-0494, and NSERC grants 69-3378, 69-0259, and 69-1325.
References
REFERENCES
- 11
- Cited by

