Hostname: page-component-745bb68f8f-kw2vx Total loading time: 0 Render date: 2025-02-06T04:31:15.341Z Has data issue: false hasContentIssue false
  • English
  • Français

Normality and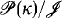

Published online by Cambridge University Press:  12 March 2014

R. Zrotowski
R. Zrotowski*
Affiliation:
Department of Mathematics, University of Wisconsin, Madison, Wisconsin 53706
Get access Rights & Permissions [Opens in a new window]

Abstract

The main result of this paper is that if κ is not a weakly Mahlo cardinal, then the following two conditions are equivalent:

1. 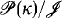is κ+-complete.

2. 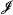is a prenormal ideal.

Our result is a generalization of an announcement made in [Z]. We say that 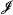is selective iff for every 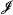-function f: κ → κ there is a set X ∈ 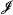such that f∣(κ − X) is one-to-one. Our theorem provides a positive partial answer to a question of B. Wȩglorz from [BTW, p. 90], viz.: is every selective ideal 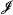with 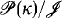κ+-complete, isomorphic to a normal ideal?

The theorem is also true for fine ideals on [λ]<κ for any κ ≤ λ, i.e. if κ is not a weakly Mahlo cardinal then the Boolean algebra 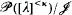is λ+-complete iff 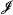is a prenormal ideal (in the sense of [λ/<κ).

Type
Research Article
Information
The Journal of Symbolic Logic , Volume 56 , Issue 3 , September 1991 , pp. 1064 - 1067
Copyright
Copyright © Association for Symbolic Logic 1991

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[BTW] Baumgartner, J., Taylor, A., and Wagon, S., Structural properties of ideals, Dissertationes Mathematicae Rozprawy Matematyczne, vol. 197 (1982).Google Scholar
[CWZ] Cichoń, J., Wȩglorz, B., and Zrotowski, R., Some properties of filters. II, Preprint No. 12, Mathematical Institute, University of Wrocław, Wrocław, 1984.Google Scholar
[W] Wȩglorz, B., Some properties of filters, Set theory and hierarchy theory. V, Lecture Notes in Mathematics, vol. 619, Springer-Verlag, Berlin, 1977, pp. 311–328.CrossRefGoogle Scholar
[Z] Zrotowski, R., A characterization of normal ideals, Abstracts of Papers Presented to the American Mathematical Society, vol. 4 (1983), p. 386.Google Scholar