Article contents
Lebesque measure zero subsets of the real line and an infinite game
Published online by Cambridge University Press: 12 March 2014
Extract
Let 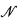 denote the ideal of Lebesgue measure zero subsets of the real line. Then add(
denote the ideal of Lebesgue measure zero subsets of the real line. Then add(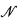 ) denotes the minimal cardinality of a subset of
) denotes the minimal cardinality of a subset of 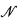 whose union is not an element of
whose union is not an element of 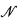 . In [1] Bartoszynski gave an elegant combinatorial characterization of add(
. In [1] Bartoszynski gave an elegant combinatorial characterization of add(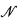 ), namely: add(
), namely: add(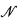 ) is the least cardinal number κ for which the following assertion fails:
) is the least cardinal number κ for which the following assertion fails:
For every family 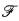 of at mostκ functions from ω to ω there is a function F from ω to the finite subsets of ω such that:
of at mostκ functions from ω to ω there is a function F from ω to the finite subsets of ω such that:
1. For each m, F(m) has at most m + 1 elements, and
2. for each f in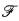 there are only finitely many m such that f(m) is not an element of F(m).
there are only finitely many m such that f(m) is not an element of F(m).
The symbol A(κ) will denote the assertion above about κ. In the course of his proof, Bartoszynski also shows that the cardinality restriction in 1 is not sharp. Indeed, let (Rm: m < ω) be any sequence of integers such that for each m Rm, ≤ Rm+1, and such that limm→∞Rm = ∞. Then the truth of the assertion A(κ) is preserved if in 1 we say instead that
1′. For each m, F(m) has at most Rm elements.
We shall use this observation later on. We now define three more statements, denoted B(κ), C(κ) and D(κ), about cardinal number κ.
Information
- Type
- Research Article
- Information
- Copyright
- Copyright © Association for Symbolic Logic 1996
References
REFERENCES
- 2
- Cited by

