Article contents
The isomorphism property in nonstandard analysis and its use in the theory of Banach spaces
Published online by Cambridge University Press: 12 March 2014
Extract
The basic setting of nonstandard analysis consists of a set-theoretical structure 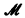 together with a map * from
together with a map * from 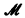 into another structure *
into another structure *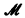 of the same sort. The function * is taken to be an elementary embedding (in an appropriate sense) and is generally assumed to make *
of the same sort. The function * is taken to be an elementary embedding (in an appropriate sense) and is generally assumed to make *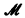 into an enlargement of
into an enlargement of 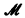 [13]. The structures
[13]. The structures 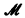 and *
and *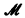 may be type-hierarchies as in [11] and [13] or they may be cumulative structures with ω levels as in [14]. The assumption that *
may be type-hierarchies as in [11] and [13] or they may be cumulative structures with ω levels as in [14]. The assumption that *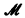 is an enlargement of
is an enlargement of 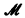 has been found to be the weakest hypothesis which allows for the familiar applications of nonstandard analysis in calculus, elementary topology, etc. Indeed, practice has shown that a smooth and useful theory can be achieved only by assuming also that *
has been found to be the weakest hypothesis which allows for the familiar applications of nonstandard analysis in calculus, elementary topology, etc. Indeed, practice has shown that a smooth and useful theory can be achieved only by assuming also that *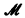 has some stronger properties such as the saturation properties first introduced in nonstandard analysis by Luxemburg [11].
has some stronger properties such as the saturation properties first introduced in nonstandard analysis by Luxemburg [11].
This paper concerns an entirely new family of properties, stronger than the saturation properties. For each cardinal number κ, *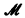 satisfies the κ-isomorphism property (as an enlargement of
satisfies the κ-isomorphism property (as an enlargement of 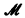 ) if the following condition holds:
) if the following condition holds:
For each first order language L with fewer than κ nonlogical symbols, if 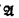 and
and 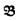 are elementarily equivalent structures for L whose domains, relations and functions are all internal (relative to *
are elementarily equivalent structures for L whose domains, relations and functions are all internal (relative to *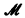 and
and 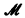 ), then
), then 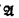 and
and 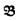 are isomorphic.
are isomorphic.
Information
- Type
- Research Article
- Information
- Copyright
- Copyright © Association for Symbolic Logic 1974
References
REFERENCES
- 24
- Cited by

