No CrossRef data available.
Article contents
INTERPRETING ARITHMETIC IN THE FIRST-ORDER THEORY OF ADDITION AND COPRIMALITY OF POLYNOMIAL RINGS
Published online by Cambridge University Press: 09 May 2019
Abstract
We study the first-order theory of polynomial rings over a GCD domain and of the ring of formal entire functions over a non-Archimedean field in the language 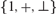 $\{ 1, + , \bot \}$. We show that these structures interpret the first-order theory of the semi-ring of natural numbers. Moreover, this interpretation depends only on the characteristic of the original ring, and thus we obtain uniform undecidability results for these polynomial and entire functions rings of a fixed characteristic. This work enhances results of Raphael Robinson on essential undecidability of some polynomial or formal power series rings in languages that contain no symbols related to the polynomial or power series ring structure itself.
$\{ 1, + , \bot \}$. We show that these structures interpret the first-order theory of the semi-ring of natural numbers. Moreover, this interpretation depends only on the characteristic of the original ring, and thus we obtain uniform undecidability results for these polynomial and entire functions rings of a fixed characteristic. This work enhances results of Raphael Robinson on essential undecidability of some polynomial or formal power series rings in languages that contain no symbols related to the polynomial or power series ring structure itself.
Information
- Type
- Articles
- Information
- Copyright
- Copyright © The Association for Symbolic Logic 2019

