Article contents
INDEPENDENCE IN GENERIC INCIDENCE STRUCTURES
Published online by Cambridge University Press: 15 February 2019
Abstract
We study the theory Tm,n of existentially closed incidence structures omitting the complete incidence structure Km,n, which can also be viewed as existentially closed Km,n-free bipartite graphs. In the case m = n = 2, this is the theory of existentially closed projective planes. We give an 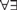 $\forall \exists$-axiomatization of Tm,n, show that Tm,n does not have a countable saturated model when m, n ≥ 2, and show that the existence of a prime model for T2,2 is equivalent to a longstanding open question about finite projective planes. Finally, we analyze model theoretic notions of complexity for Tm,n. We show that Tm,n is NSOP1, but not simple when m, n ≥ 2, and we show that Tm,n has weak elimination of imaginaries but not full elimination of imaginaries. These results rely on combinatorial characterizations of various notions of independence, including algebraic independence, Kim independence, and forking independence.
$\forall \exists$-axiomatization of Tm,n, show that Tm,n does not have a countable saturated model when m, n ≥ 2, and show that the existence of a prime model for T2,2 is equivalent to a longstanding open question about finite projective planes. Finally, we analyze model theoretic notions of complexity for Tm,n. We show that Tm,n is NSOP1, but not simple when m, n ≥ 2, and we show that Tm,n has weak elimination of imaginaries but not full elimination of imaginaries. These results rely on combinatorial characterizations of various notions of independence, including algebraic independence, Kim independence, and forking independence.
Keywords
Information
- Type
- Articles
- Information
- Copyright
- Copyright © The Association for Symbolic Logic 2019
References
REFERENCES
- 7
- Cited by

