Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Czajka, Łukasz
2013.
Foundations of Software Science and Computation Structures.
Vol. 7794,
Issue. ,
p.
177.
CAIE, MICHAEL
2020.
BUNDER’S PARADOX.
The Review of Symbolic Logic,
Vol. 13,
Issue. 4,
p.
829.

 thus establishing its strong consistency. We also use a variant of this construction to provide a complete embedding of first-order intuitionistic predicate logic with second-order propositional quantifiers into the system
thus establishing its strong consistency. We also use a variant of this construction to provide a complete embedding of first-order intuitionistic predicate logic with second-order propositional quantifiers into the system 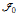 of Barendregt, Bunder and Dekkers, which gives a partial answer to a question posed by these authors.
of Barendregt, Bunder and Dekkers, which gives a partial answer to a question posed by these authors.