Article contents
THE GENERIC DEGREES OF DENSITY-1 SETS, AND A CHARACTERIZATION OF THE HYPERARITHMETIC REALS
Published online by Cambridge University Press: 22 December 2015
Abstract
A generic computation of a subset A of ℕ is a computation which correctly computes most of the bits of A, but which potentially does not halt on all inputs. The motivation for this concept is derived from complexity theory, where it has been noticed that frequently, it is more important to know how difficult a type of problem is in the general case than how difficult it is in the worst case. When we study this concept from a recursion theoretic point of view, to create a transitive relationship, we are forced to consider oracles that sometimes fail to give answers when asked questions. Unfortunately, this makes working in the generic degrees quite difficult. Indeed, we show that generic reduction is 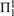 $\Pi _1^1$―complete. To help avoid this difficulty, we work with the generic degrees of density-1 reals. We demonstrate how an understanding of these degrees leads to a greater understanding of the overall structure of the generic degrees, and we also use these density-1 sets to provide a new a characterization of the hyperartithmetical Turing degrees.
$\Pi _1^1$―complete. To help avoid this difficulty, we work with the generic degrees of density-1 reals. We demonstrate how an understanding of these degrees leads to a greater understanding of the overall structure of the generic degrees, and we also use these density-1 sets to provide a new a characterization of the hyperartithmetical Turing degrees.
Information
- Type
- Articles
- Information
- Copyright
- Copyright © The Association for Symbolic Logic 2015
References
REFERENCES
- 8
- Cited by

