Article contents
GENERIC CODING WITH HELP AND AMALGAMATION FAILURE
Published online by Cambridge University Press: 05 October 2020
Abstract
We show that if M is a countable transitive model of  $\text {ZF}$ and if
$\text {ZF}$ and if 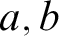 $a,b$ are reals not in M, then there is a G generic over M such that
$a,b$ are reals not in M, then there is a G generic over M such that 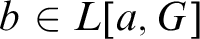 $b \in L[a,G]$. We then present several applications such as the following: if J is any countable transitive model of
$b \in L[a,G]$. We then present several applications such as the following: if J is any countable transitive model of 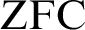 $\text {ZFC}$ and
$\text {ZFC}$ and 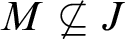 $M \not \subseteq J$ is another countable transitive model of
$M \not \subseteq J$ is another countable transitive model of 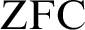 $\text {ZFC}$ of the same ordinal height
$\text {ZFC}$ of the same ordinal height 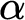 $\alpha $, then there is a forcing extension N of J such that
$\alpha $, then there is a forcing extension N of J such that  $M \cup N$ is not included in any transitive model of
$M \cup N$ is not included in any transitive model of 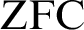 $\text {ZFC}$ of height
$\text {ZFC}$ of height 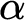 $\alpha $. Also, assuming
$\alpha $. Also, assuming 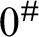 $0^{\#}$ exists, letting S be the set of reals generic over L, although S is disjoint from the Turing cone above
$0^{\#}$ exists, letting S be the set of reals generic over L, although S is disjoint from the Turing cone above 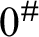 $0^{\#}$, we have that for any non-constructible real a,
$0^{\#}$, we have that for any non-constructible real a, 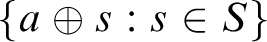 $\{ a \oplus s : s \in S \}$ is cofinal in the Turing degrees.
$\{ a \oplus s : s \in S \}$ is cofinal in the Turing degrees.
Information
- Type
- Article
- Information
- Copyright
- © Association for Symbolic Logic 2020
References
- 1
- Cited by


