Published online by Cambridge University Press: 12 March 2014
We present some abstract theorems showing how domination properties equivalent to being 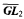 or array nonrecursive can be used to construct sets generic for different notions of forcing. These theorems are then applied to give simple proofs of some known results. We also give a direct uniform proof of a recent result of Ambos-Spies, Ding, Wang, and Yu [2009] that every degree above any in
or array nonrecursive can be used to construct sets generic for different notions of forcing. These theorems are then applied to give simple proofs of some known results. We also give a direct uniform proof of a recent result of Ambos-Spies, Ding, Wang, and Yu [2009] that every degree above any in 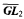 is recursively enumerable in a 1-generic degree strictly below it. Our major new result is that every array nonrecursive degree is r.e. in some degree strictly below it. Our analysis of array nonrecursiveness and construction of generic sequences below ANR degrees also reveal a new level of uniformity in these types of results.
is recursively enumerable in a 1-generic degree strictly below it. Our major new result is that every array nonrecursive degree is r.e. in some degree strictly below it. Our analysis of array nonrecursiveness and construction of generic sequences below ANR degrees also reveal a new level of uniformity in these types of results.