Article contents
COMPUTABILITY IN UNCOUNTABLE BINARY TREES
Published online by Cambridge University Press: 12 March 2019
Abstract
Computability, while usually performed within the context of ω, may be extended to larger ordinals by means of α-recursion. In this article, we concentrate on the particular case of ω1-recursion, and study the differences in the behavior of 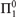 ${\rm{\Pi }}_1^0$-classes between this case and the standard one.
${\rm{\Pi }}_1^0$-classes between this case and the standard one.
Of particular interest are the 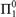 ${\rm{\Pi }}_1^0$-classes corresponding to computable trees of countable width. Classically, it is well-known that the analog to König’s Lemma—“every tree of countable width and uncountable height has an uncountable branch”—fails; we demonstrate that not only does it fail effectively, but also that the failure is as drastic as possible. This is proven by showing that the ω1-Turing degrees of even isolated paths in computable trees of countable width are cofinal in the
${\rm{\Pi }}_1^0$-classes corresponding to computable trees of countable width. Classically, it is well-known that the analog to König’s Lemma—“every tree of countable width and uncountable height has an uncountable branch”—fails; we demonstrate that not only does it fail effectively, but also that the failure is as drastic as possible. This is proven by showing that the ω1-Turing degrees of even isolated paths in computable trees of countable width are cofinal in the  ${\rm{\Delta }}_1^1\,{\omega _1}$-Turing degrees.
${\rm{\Delta }}_1^1\,{\omega _1}$-Turing degrees.
Finally, we consider questions of nonisolated paths, and demonstrate that the degrees realizable as isolated paths and the degrees realizable as nonisolated ones are very distinct; in particular, we show that there exists a computable tree of countable width so that every branch can only be ω1-Turing equivalent to branches of trees with 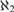 ${\aleph _2}$-many branches.
${\aleph _2}$-many branches.
Information
- Type
- Articles
- Information
- Copyright
- Copyright © The Association for Symbolic Logic 2019
References
REFERENCES
- 1
- Cited by

