No CrossRef data available.
Article contents
The complexity of the core model
Published online by Cambridge University Press: 12 March 2014
Abstract
If there is no inner model with a cardinal κ such that ο(κ) = κ ++ then the set K ∩ H ω1 is definable over H ω1 by a Δ4 formula, and the set 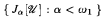 of countable initial segments of the core model
of countable initial segments of the core model 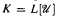 is definable over H ω1 by a Π3 formula. We show that if there is an inner model with infinitely many measurable cardinals then there is a model in which
is definable over H ω1 by a Π3 formula. We show that if there is an inner model with infinitely many measurable cardinals then there is a model in which 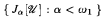 is not definable Σ3 by any Σ3 formula, and K ∩ H ω1 is not definable by any boolean combination of Σ3 formulas.
is not definable Σ3 by any Σ3 formula, and K ∩ H ω1 is not definable by any boolean combination of Σ3 formulas.
Information
- Type
- Research Article
- Information
- Copyright
- Copyright © Association for Symbolic Logic 1998
References
REFERENCES
[1]
Mitchell, William J., The core model for sequences of measures, Mathematics Proceedings of the Cambridge Philosophical Society, vol. 95 (1984), pp. 41—58.CrossRefGoogle Scholar
[2]
Mitchell, William J.,
Σ1
3
absoluteness for sequences of measures, Set theory of the continuum (Judah, H., Just, W., and Woodin, W. Hugh, editors), Springer-Verlag, Berlin, 1992, pp. 311—355.CrossRefGoogle Scholar
[3]
Mitchell, William J. and Steel, John R., Fine structure and iteration trees, ASL Lecture Notes in Logic, vol. 3, Springer-Verlag, Berline, 1994.CrossRefGoogle Scholar
[4]
Steel, John R., The core model iterahility problem, ASL Lecture Notes in Logic, vol. 8, Springer-Verlag, 1996.CrossRefGoogle Scholar

