Hostname: page-component-7dd5485656-wjfd9 Total loading time: 0 Render date: 2025-10-29T21:59:30.212Z Has data issue: false hasContentIssue false
  • English
  • Français

THE COMPLEXITY OF SCOTT SENTENCES OF SCATTERED LINEAR ORDERS

Part of: Model theory Computability and recursion theory

Published online by Cambridge University Press:  23 October 2020

RACHAEL ALVIR  and
DINO ROSSEGGER
RACHAEL ALVIR
Affiliation:
DEPARTMENT OF MATHEMATICS UNIVERSITY OF NOTRE DAME NOTRE DAME, IN, USA E-mail: ralvir@nd.edu
DINO ROSSEGGER
Affiliation:
DEPARTMENT OF PURE MATHEMATICS UNIVERSITY OF WATERLOO WATERLOO, CANADA E-mail: drossegg@uwaterloo.ca
Get access Rights & Permissions [Opens in a new window]

Abstract

We calculate the complexity of Scott sentences of scattered linear orders. Given a countable scattered linear order L of Hausdorff rank 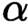$\alpha $ we show that it has a 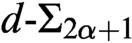${d\text {-}\Sigma _{2\alpha +1}}$ Scott sentence. It follows from results of Ash [2] that for every countable 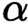$\alpha $ there is a linear order whose optimal Scott sentence has this complexity. Therefore, our bounds are tight. We furthermore show that every Hausdorff rank 1 linear order has an optimal 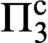${\Pi ^{\mathrm {c}}_{3}}$ or 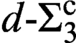${d\text {-}\Sigma ^{\mathrm {c}}_{3}}$ Scott sentence and give a characterization of those linear orders of rank 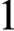$1$ with 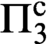${\Pi ^{\mathrm {c}}_{3}}$ optimal Scott sentences. At last we show that for all countable 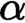$\alpha $ the class of Hausdorff rank 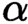$\alpha $ linear orders is 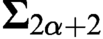$\boldsymbol {\Sigma }_{2\alpha +2}$ complete and obtain analogous results for index sets of computable linear orders.

Keywords

Scott ranklinear ordersscattered linear ordersHausdorff rank

MSC classification

Primary: 03C75: Other infinitary logic
Secondary: 03D45: Theory of numerations, effectively presented structures

Information

Type
Articles
Information
The Journal of Symbolic Logic , Volume 85 , Issue 3 , September 2020 , pp. 1079 - 1101
Check for updates
Copyright
© The Association for Symbolic Logic 2020

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

REFERENCES

Alvir, R., Knight, J., and McCoy, C., Complexity of Scott sentences , Fundamenta Mathematicae , vol. 251 (2020), pp. 109–129.CrossRefGoogle Scholar
Ash, C., Recursive labelling systems and stability of recursive structures in hyperarithmetical degrees . Transactions of the American Mathematical Society , vol. 298 (1986), no. 2, pp. 497–514.CrossRefGoogle Scholar
Ash, C. and Knight, J., Computable Structures and the Hyperarithmetical Hierarchy , Studies in Logic and the Foundations of Mathematics, vol. 144, Elsevier Science, Amsterdam, 2000.Google Scholar
Ash, C. and Knight, J., Pairs of recursive structures . Annals of Pure and Applied Logic 46 (1990), no. 3, pp. 211–234.CrossRefGoogle Scholar
Calvert, W., Knight, J., and Millar, J., Computable trees of Scott rank  ${\omega}_1^{ck}$ , and computable approximation, this Journal, vol. 71 (2006), no. 1, pp. 283–298.Google Scholar
Calvert, W., Harizanov., V. S., Knight, J. F., and Miller, S., Index sets of computable structures . Algebra and Logic , vol. 45 (2006), no. 5, pp. 306–325.CrossRefGoogle Scholar
Harrison, J., Recursive pseudo-well-orderings . Transactions of the American Mathematical Society , vol. 131 (1968), no. 2, pp. 526–543.CrossRefGoogle Scholar
Harrison-Trainor, M., Igusa, G., and Knight, J., Some new computable structures of high rank . Proceedings of the American Mathematical Society , vol. 146 (2018), no. 7, pp. 3097–3109.CrossRefGoogle Scholar
Hausdorff, F., Grundzüge einer Theorie der geordneten Mengen . Mathematische Annalen , vol. 65 (1908), no. 4, pp. 435–505.CrossRefGoogle Scholar
Kechris, A., Classical Descriptive Set Theory , Springer, Berlin, 2012.Google Scholar
Knight, J. and McCoy, C., Index sets and Scott sentences . Archive for Mathematical Logic , vol. 53 (2014), no. 5–6, pp. 519–524.CrossRefGoogle Scholar
Knight, J. and Millar, J., Computable structures of rank  ${\omega}_1^{ck}$ . Journal of Mathematical Logic , vol. 10 (2010), no. 1, pp. 31–43.CrossRefGoogle Scholar
McCoy, C., ${\varDelta}_2^0$ -categoricity in boolean algebras and linear orderings . Annals of Pure and Applied Logic , vol. 119 (2003), no. 1, pp. 85–120.CrossRefGoogle Scholar
Miller, A., On the borel classification of the isomorphism class of a countable model . Notre Dame Journal of Formal Logic , vol. 24 (1983), no. 1, pp. 22–34.CrossRefGoogle Scholar
Miller, R., Revisiting uniform computable categoricity: for the sixtieth birthday of prof. Rod Downey , Computability and Complexity (Day, A., Fellows, M., Greenberg, N., Khoussainov, B., Melnikov, A., and Rosamond, R., editors), Springer, Cham, 2017, pp. 254–270.CrossRefGoogle Scholar
Montalbán, A., A Robuster Scott rank . Proceedings of the American Mathematical Society , vol. 143 (2015), no. 12, pp. 5427–5436.CrossRefGoogle Scholar
Montalbán, A., Up to equimorphism, hyperarithmetic is recursive, this Journal, vol. 70 (2005), no. 2, pp. 360–378.Google Scholar
Nadel, M., Scott sentences and admissible sets . Annals of Mathematical Logic , vol. 7 (1974), no. 2, pp. 267–294.CrossRefGoogle Scholar
Scott, D., Logic with denumerably long formulas and finite strings of quantifiers , The Theory of Models (Addison, J., Henkin, L., and Tarski, A., editors), North-Holland, Amsterdam, 1965, pp. 329–341.Google Scholar
Soare, R. I., Turing Computability. Theory and Applications of Computability , Springer, Berlin, Heidelberg, 2016.Google Scholar
Vaught, R., Invariant sets in topology and logic . Fundamenta Mathematicae , vol. 82 (1974), pp. 269–294.CrossRefGoogle Scholar