Published online by Cambridge University Press: 12 August 2016
Schweber [10] defined a reducibility that allows us to compare the computing power of structures of arbitrary cardinality. Here we focus on the ordered field 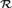 ${\cal R}$ of real numbers and a structure
${\cal R}$ of real numbers and a structure 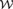 ${\cal W}$ that just codes the subsets of ω. In [10], it was observed that
${\cal W}$ that just codes the subsets of ω. In [10], it was observed that 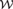 ${\cal W}$ is reducible to
${\cal W}$ is reducible to 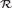 ${\cal R}$ . We prove that
${\cal R}$ . We prove that 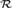 ${\cal R}$ is not reducible to
${\cal R}$ is not reducible to 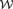 ${\cal W}$ . As part of the proof, we show that for a countable recursively saturated real closed field
${\cal W}$ . As part of the proof, we show that for a countable recursively saturated real closed field 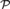 ${\cal P}$ with residue field k, some copy of
${\cal P}$ with residue field k, some copy of 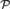 ${\cal P}$ does not compute a copy of k.
${\cal P}$ does not compute a copy of k.