Article contents
A 1-generic degree with a strong minimal cover
Published online by Cambridge University Press: 12 March 2014
Extract
We consider a set generic over the arithmetic sets. A subset A of the natural numbers is called n-generic if it is Cohen-generic for n-quantifier arithmetic. This is equivalent to saying that for every 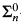 -set of strings S, there is a string σ ⊂ A such that σ ∈ S or no extension of σ is in S. By degree we mean Turing degree (of unsolvability). We call a degree n-generic if it has an n-generic representative. For a degree a, let D(≤ a) denote the set of degrees which are recursive in a.
-set of strings S, there is a string σ ⊂ A such that σ ∈ S or no extension of σ is in S. By degree we mean Turing degree (of unsolvability). We call a degree n-generic if it has an n-generic representative. For a degree a, let D(≤ a) denote the set of degrees which are recursive in a.
We say a is a strong minimal cover of g if every degree strictly below a is less than or equal to g. In this paper we show that there are a 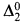 degree a and a 1-generic degree g < a such that a is a strong minimal cover of g. This easily implies that there is a 1-generic degree without the cupping property. Jockusch [7] showed that every 2-generic degree has the cupping property. Slaman and Steel [17] and independently Cooper [3] showed that there are recursively enumerable degrees a and b < a such that no degree c < a joins b above a. Take a 1-generic degree g below b. Then g does not have the cupping property.
degree a and a 1-generic degree g < a such that a is a strong minimal cover of g. This easily implies that there is a 1-generic degree without the cupping property. Jockusch [7] showed that every 2-generic degree has the cupping property. Slaman and Steel [17] and independently Cooper [3] showed that there are recursively enumerable degrees a and b < a such that no degree c < a joins b above a. Take a 1-generic degree g below b. Then g does not have the cupping property.
Information
- Type
- Research Article
- Information
- Copyright
- Copyright © Association for Symbolic Logic 2000
References
REFERENCES
- 4
- Cited by

