Article contents
Stability of a tokamak plasma with diffuse toroidal rotation
Published online by Cambridge University Press: 20 October 2020
Abstract
The present work considers the stability of a high-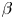 $\beta$, large aspect ratio, circular plasma with diffuse profiles for the safety factor and the angular toroidal frequency (López & Guazzotto, Phys. Plasmas, vol. 24, 032501). An application of the Frieman–Rotenberg formalism results in a system of scalar eigenmode equations whose coupling is retained at the plasma–vacuum transition but is disregarded across the plasma column, which is a standard practice. The solution technique consists of a multidimensional shooting method for the poloidal harmonics; robust initial guesses are constructed by solving the dispersion relation in the static scenario with vanishing magnetic shear. Flow shear appears as a high-
$\beta$, large aspect ratio, circular plasma with diffuse profiles for the safety factor and the angular toroidal frequency (López & Guazzotto, Phys. Plasmas, vol. 24, 032501). An application of the Frieman–Rotenberg formalism results in a system of scalar eigenmode equations whose coupling is retained at the plasma–vacuum transition but is disregarded across the plasma column, which is a standard practice. The solution technique consists of a multidimensional shooting method for the poloidal harmonics; robust initial guesses are constructed by solving the dispersion relation in the static scenario with vanishing magnetic shear. Flow shear appears as a high-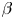 $\beta$ toroidal contribution, and we illustrate its destabilizing influence on
$\beta$ toroidal contribution, and we illustrate its destabilizing influence on  $n=1$ external kink modes in the presence of ideal and resistive walls. Internal resonances are avoided by means of the selection of appropriate equilibrium parameters. The stabilizing influence of a finite positive average magnetic shear is also exemplified.
$n=1$ external kink modes in the presence of ideal and resistive walls. Internal resonances are avoided by means of the selection of appropriate equilibrium parameters. The stabilizing influence of a finite positive average magnetic shear is also exemplified.
Information
- Type
- Research Article
- Information
- Copyright
- Copyright © The Author(s), 2020. Published by Cambridge University Press
References
REFERENCES
- 1
- Cited by


