Article contents
On magnetic helicity generation and transport in a nonlinear dynamo driven by a helical flow
Published online by Cambridge University Press: 27 August 2020
Abstract
The relationship between nonlinear large-scale dynamo action and the generation and transport of magnetic helicity is investigated at moderate values of the magnetic Reynolds number (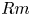 $Rm$). The model consists of a helically forced, sheared flow in a Cartesian domain. The boundary conditions are periodic in the horizontal and impenetrable for the vertical. The magnetic field is required to be vertical at the upper and lower boundaries. There are two consequences of this choice; one is that the magnetic helicity is not gauge invariant, the second is that fluxes of magnetic helicity are allowed in and out of the domain. We select the winding gauge, define all the contributions to the evolution of the helicity in this gauge and measure these contributions for various solutions of the dynamo equations. We vary
$Rm$). The model consists of a helically forced, sheared flow in a Cartesian domain. The boundary conditions are periodic in the horizontal and impenetrable for the vertical. The magnetic field is required to be vertical at the upper and lower boundaries. There are two consequences of this choice; one is that the magnetic helicity is not gauge invariant, the second is that fluxes of magnetic helicity are allowed in and out of the domain. We select the winding gauge, define all the contributions to the evolution of the helicity in this gauge and measure these contributions for various solutions of the dynamo equations. We vary 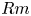 $Rm$ and the shear strength, and find a rich landscape of dynamo solutions including travelling waves, pulsating waves and non-wave-like solutions. We find that, at the
$Rm$ and the shear strength, and find a rich landscape of dynamo solutions including travelling waves, pulsating waves and non-wave-like solutions. We find that, at the 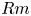 $Rm$ considered, the main contribution to the growth of magnetic helicity comes from processes throughout the volume of the fluid and that boundary terms respond by limiting the growth. We find that, in this magnetic Reynolds number regime, helicity conservation is not a strong constraint on large-scale dynamo action. We speculate on what may happen at higher
$Rm$ considered, the main contribution to the growth of magnetic helicity comes from processes throughout the volume of the fluid and that boundary terms respond by limiting the growth. We find that, in this magnetic Reynolds number regime, helicity conservation is not a strong constraint on large-scale dynamo action. We speculate on what may happen at higher 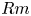 $Rm$.
$Rm$.
Keywords
Information
- Type
- Research Article
- Information
- Copyright
- Copyright © The Author(s), 2020. Published by Cambridge University Press
References
REFERENCES
- 6
- Cited by

