Article contents
Merging of the superbanana plateau and $\sqrt \nu$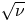 transport regimes in nearly quasisymmetric stellarators
transport regimes in nearly quasisymmetric stellarators
Published online by Cambridge University Press: 19 January 2023
Abstract
Alpha particle confinement is one of the most demanding issues for stellarators. It now seems clear that it is possible to design optimized stellarators that confine the background plasma at near tokamak radial transport levels. Moreover, adequate collisionless alpha particle confinement is possible in the core of a highly optimized stellarator. Here, the collisional confinement of barely trapped alphas in an optimized stellarator is considered by accounting for the resonance due to the reversal in direction of the drift within a flux surface and investigating the sensitive role of magnetic shear in keeping this resonance close to the passing boundary in some nearly quasisymmetric stellarator configurations. The treatment relies on a narrow collisional boundary layer formulation that combines the responses of both these resonant pitch angle alphas and the remaining barely trapped alphas. A novel merged regime treatment leads to explicit expressions for the energy diffusivity for both superbanana plateau (or resonant plateau) and $\sqrt \nu$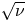 transport in the large aspect ratio limit for a slowing down tail alpha distribution function, where $\nu$
transport in the large aspect ratio limit for a slowing down tail alpha distribution function, where $\nu$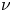 is the effective pitch angle scattering collision frequency of the trapped alphas off the background ions. Depending on the details of the optimization scheme and the sign of the magnetic shear, modest magnetic shear can be used to reduce superbanana (or resonant) plateau transport to below the $\sqrt \nu$
is the effective pitch angle scattering collision frequency of the trapped alphas off the background ions. Depending on the details of the optimization scheme and the sign of the magnetic shear, modest magnetic shear can be used to reduce superbanana (or resonant) plateau transport to below the $\sqrt \nu$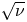 transport level. In addition, a quasilinear equation retaining spatial diffusion is derived for a general alpha distribution function that allows the radial alpha transport to modify the distribution so it is no longer isotropic in velocity space.
transport level. In addition, a quasilinear equation retaining spatial diffusion is derived for a general alpha distribution function that allows the radial alpha transport to modify the distribution so it is no longer isotropic in velocity space.
Keywords
Information
- Type
- Research Article
- Information
- Copyright
- Copyright © The Author(s), 2023. Published by Cambridge University Press
References
- 3
- Cited by


