Article contents
Local fluxes in magnetohydrodynamic turbulence
Published online by Cambridge University Press: 02 November 2022
Abstract
Using highly resolved direct numerical simulations we examine the statistical properties of the local energy flux rate $\varPi _\ell (x)$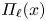 towards small scales for three isotropic turbulent magnetohydrodynamic flows, which differ in strength and structure of the magnetic field. We analyse the cascade process in both kinetic and magnetic energy, disentangling the different flux contributions to the overall energy dynamics. The results show that the probability distribution of the local energy flux develops long tails related to extreme events, similar to the hydrodynamic case. The different terms of the energy flux display different properties and show sensitivity to the type of the flow examined. We further examine the joint probability density function between the local energy flux and the gradients of the involved fields. The results point out a correlation with the magnetic field gradients, showing, however, a dispersion much stronger than what is observed in hydrodynamic flows. Finally, it is also shown that the local energy flux shows some dependence on the local amplitude of the magnetic field. The present results have implications for subgrid-scale models, which we discuss.
towards small scales for three isotropic turbulent magnetohydrodynamic flows, which differ in strength and structure of the magnetic field. We analyse the cascade process in both kinetic and magnetic energy, disentangling the different flux contributions to the overall energy dynamics. The results show that the probability distribution of the local energy flux develops long tails related to extreme events, similar to the hydrodynamic case. The different terms of the energy flux display different properties and show sensitivity to the type of the flow examined. We further examine the joint probability density function between the local energy flux and the gradients of the involved fields. The results point out a correlation with the magnetic field gradients, showing, however, a dispersion much stronger than what is observed in hydrodynamic flows. Finally, it is also shown that the local energy flux shows some dependence on the local amplitude of the magnetic field. The present results have implications for subgrid-scale models, which we discuss.
Keywords
Information
- Type
- Research Article
- Information
- Copyright
- Copyright © The Author(s), 2022. Published by Cambridge University Press
References
REFERENCES
- 3
- Cited by


