Hostname: page-component-745bb68f8f-b6zl4 Total loading time: 0 Render date: 2025-01-11T03:56:11.088Z Has data issue: false hasContentIssue false
  • English
  • Français

Hydrodynamics of quantum corrections to the Coulomb interaction via the third rank tensor evolution equation: application to Langmuir waves and spin-electron acoustic waves

Published online by Cambridge University Press:  04 November 2021

Pavel A. Andreev Open the ORCID record for Pavel A. Andreev [Opens in a new window]
Pavel A. Andreev*
Affiliation:
Faculty of Physics, Lomonosov Moscow State University, Moscow 119991, Russian Federation Faculty of Physics, Mathematics and Natural Sciences, Peoples Friendship University of Russia (RUDN University), 6 Miklukho-Maklaya Street, Moscow 117198, Russian Federation
*
†Email address for correspondence: andreevpa@physics.msu.ru
Get access Rights & Permissions [Opens in a new window]

Abstract

The quantum effects in plasmas can be described by the hydrodynamics containing the continuity and Euler equations. However, novel quantum phenomena are found via the extended set of hydrodynamic equations, where the pressure evolution equation and the pressure flux third-rank tensor evolution equation are included. These give the quantum corrections to the Coulomb interaction. The spectra of the Langmuir waves and the spin-electron acoustic waves are calculated. The application of the pressure evolution equation ensures that the contribution of pressure in the Langmuir wave spectrum is proportional to $(3/5)v_{\textrm {Fe}}^{2}$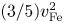 rather than $(1/3)v_{\textrm {Fe}}^{2}$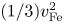, where $v_{\textrm {Fe}}$ 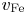is the Fermi velocity.

Keywords

plasmasgeneral fluid mechanicsquantum fluids
Type
Research Article
Information
Journal of Plasma Physics , Volume 87 , Issue 5 , October 2021 , 905870511
Check for updates
Copyright
Copyright © The Author(s), 2021. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Aleksandrov, A.F., Bogdankevich, L.S. & Rukhadze, A.A. 1984 Principles of Plasma Electrodynamics. Springer.CrossRefGoogle Scholar
Anderson, D., Hall, B., Lisak, M. & Marklund, M. 2002 Statistical effects in the multistream model for quantum plasmas. Phys. Rev. E 65, 046417.CrossRefGoogle ScholarPubMed
Andreev, P.A. 2015 Separated spin-up and spin-down quantum hydrodynamics of degenerated electrons. Phys. Rev. E 91, 033111.CrossRefGoogle ScholarPubMed
Andreev, P.A. 2016 a Spin-electron acoustic waves: the Landau damping and ion contribution in the spectrum. Phys. Plasmas 23, 062103.CrossRefGoogle Scholar
Andreev, P.A. 2016 b Spin-electron acoustic soliton and exchange interaction in separate spin evolution quantum plasmas. Phys. Plasmas 23, 012106.CrossRefGoogle Scholar
Andreev, P.A. 2017 a Kinetic analysis of spin current contribution to spectrum of electromagnetic waves in spin-1/2 plasma. I. Dielectric permeability tensor for magnetized plasmas. Phys. Plasmas 24, 022114.CrossRefGoogle Scholar
Andreev, P.A. 2017 b Kinetic analysis of spin current contribution to spectrum of electromagnetic waves in spin-1/2 plasma. II. Dispersion dependencies. Phys. Plasmas 24, 022115.CrossRefGoogle Scholar
Andreev, P.A. 2021 Quantum hydrodynamic theory of quantum fluctuations in dipolar Bose–Einstein condensate. Chaos 31, 023120.CrossRefGoogle ScholarPubMed
Andreev, P.A. & Ivanov, A.Y. 2015 Exchange Coulomb interaction in nanotubes: dispersion of Langmuir waves. Phys. Plasmas 22, 072101.CrossRefGoogle Scholar
Andreev, P.A. & Kuz'menkov, L.S. 2007 Eigenwaves in a two-component system of particles with nonzero magnetic moments. Moscow Univ. Phys. Bull. 62 (N.5), 271.CrossRefGoogle Scholar
Andreev, P.A. & Kuz'menkov, L.S. 2008 Generation of waves by a neutron beam in a two-component system formed by charged particles of nonzero spin. Phys. At. Nucl. 71 (N.10), 1724.CrossRefGoogle Scholar
Andreev, P.A. & Kuz'menkov, L.S. 2015 Oblique propagation of longitudinal waves in magnetized spin-1/2 plasmas: independent evolution of spin-up and spin-down electrons. Ann. Phys. 361, 278.CrossRefGoogle Scholar
Andreev, P.A. & Kuz'menkov, L.S. 2016 a Separated spin-up and spin-down evolution of degenerated electrons in two-dimensional systems: Dispersion of longitudinal collective excitations in plane and nanotube geometry. Eur. Phys. Lett. 113, 17001.CrossRefGoogle Scholar
Andreev, P.A. & Kuz'menkov, L.S. 2016 b Surface spin-electron acoustic waves in magnetically ordered metals. Appl. Phys. Lett. 108, 191605.CrossRefGoogle Scholar
Andreev, P.A. & Kuz'menkov, L.S. 2019 On the equation of state for the thermal part of the spin current: the Pauli principle contribution in the spin wave spectrum in a cold fermion system. Prog. Theor. Exp. Phys. 2019, 053J01.CrossRefGoogle Scholar
Brodin, G. & Marklund, M. 2007 Spin magnetohydrodynamics. New J. Phys. 9, 277.CrossRefGoogle Scholar
Golubnychiy, V., Bonitz, M., Kremp, D. & Schlanges, M. 2001 Dynamical properties and plasmon dispersion of a weakly degenerate correlated one-component plasma. Phys. Rev. E 64, 016409.CrossRefGoogle ScholarPubMed
Haas, F. 2005 A magnetohydrodynamic model for quantum plasmas. Phys. Plasmas 12, 062117.CrossRefGoogle Scholar
Haas, F., Garcia, L.G., Goedert, J. & Manfredi, G. 2003 Quantum ion-acoustic waves. Phys. Plasmas 10, 3858.CrossRefGoogle Scholar
Haas, F., Manfredi, G. & Feix, M. 2000 Multistream model for quantum plasmas. Phys. Rev. E 62, 2763.CrossRefGoogle ScholarPubMed
Jung, Y.-D. & Akbari-Moghanjoughi, M. 2014 Electron-exchange effects on the charge capture process in degenerate quantum plasmas. Phys. Plasmas 21, 032108.CrossRefGoogle Scholar
Koide, T. 2013 Spin-electromagnetic hydrodynamics and magnetization induced by spin-magnetic interaction. Phys. Rev. C 87, 034902.CrossRefGoogle Scholar
Kremp, D., Bornath, T., Bonitz, M. & Schlanges, M. 1999 Quantum kinetic theory of plasmas in strong laser fields. Phys. Rev. E 60, 4725.CrossRefGoogle ScholarPubMed
Kuz'menkov, L.S. & Maksimov, S.G. 1999 Quantum hydrodynamics of particle systems with coulomb interaction and quantum Bohm potential. Theor. Math. Phys. 118, 227.CrossRefGoogle Scholar
Kuz'menkov, L.S., Maksimov, S.G. & Fedoseev, V.V. 2001 a Microscopic quantum hydrodynamics of systems of fermions: part I. Theor. Math. Phys. 126, 110.CrossRefGoogle Scholar
Kuz'menkov, L.S., Maksimov, S.G. & Fedoseev, V.V. 2001 b Microscopic quantum hydrodynamics of systems of fermions: part II. Theor. Math. Phys. 126, 212.CrossRefGoogle Scholar
Landau, L. & Lifshitz, E.M. 1980 Statistical Physics, Part II. Pergamon.Google Scholar
Lee, G.W. & Jung, Y.-D. 2013 Electron-exchange and quantum screening effects on the Thomson scattering process in quantum Fermi plasmas. Phys. Plasmas 20, 062108.CrossRefGoogle Scholar
Mahajan, S.M. & Asenjo, F.A. 2011 Vortical dynamics of spinning quantum plasmas: helicity conservation. Phys. Rev. Lett. 107, 195003.CrossRefGoogle ScholarPubMed
Manfredi, G. 2005 How to model quantum plasmas. arXiv:quant-ph/0505004.CrossRefGoogle Scholar
Marklund, M. & Brodin, G. 2007 Dynamics of spin-1/2 quantum plasmas. Phys. Rev. Lett. 98, 025001.CrossRefGoogle ScholarPubMed
Miller, S.T. & Shumlak, U. 2016 A multi-species 13-moment model for moderately collisional plasmas. Phys. Plasmas 23, 082303.CrossRefGoogle Scholar
Moldabekov, Z.A., Bonitz, M. & Ramazanov, T.S. 2018 Theoretical foundations of quantum hydrodynamics for plasmas. Phys. Plasmas 25, 031903.CrossRefGoogle Scholar
Shokri, B. & Rukhadze, A.A. 1999 Quantum drift waves. Phys. Plasmas 6, 4467.CrossRefGoogle Scholar
Shukla, P.K. & Eliasson, B. 2010 Nonlinear aspects of quantum plasma physics. Phys. Usp. 53, 51.CrossRefGoogle Scholar
Shukla, P.K. & Eliasson, B. 2011 Nonlinear collective interactions in quantum plasmas with degenerate electron fluids. Rev. Mod. Phys. 83, 885.CrossRefGoogle Scholar
Tokatly, I. & Pankratov, O. 1999 Hydrodynamic theory of an electron gas. Phys. Rev. B 60, 15550.CrossRefGoogle Scholar
Tokatly, I.V. & Pankratov, O. 2000 Hydrodynamics beyond local equilibrium: application to electron gas. Phys. Rev. B 62, 2759.CrossRefGoogle Scholar
Uzdensky, D.A. & Rightley, S. 2014 Plasma physics of extreme astrophysical environments. Rep. Prog. Phys. 77, 036902.CrossRefGoogle ScholarPubMed
Supplementary material: PDF

Andreev supplementary material

Andreev supplementary material

Download Andreev supplementary material(PDF)
PDF 78 KB