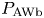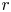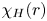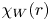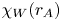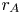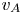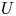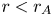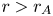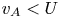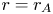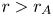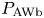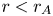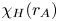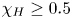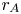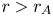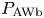1. Introduction
Following Parker's (Reference Parker1958) prediction that the Sun emits a supersonic wind, a number of studies attempted to model the solar wind as a spherically symmetric outflow powered by the outward conduction of heat from a hot coronal base (e.g. Parker Reference Parker1965; Hartle & Sturrock Reference Hartle and Sturrock1968; Durney Reference Durney1972; Roberts & Soward Reference Roberts and Soward1972). Although these studies obtained supersonic wind solutions, they were unable to reproduce the large outflow velocities measured in the fast solar wind near Earth (![]() $700\text {--}800\ \text {km}\,\text {s}^{-1}$), and they did not explain the origin of the high coronal temperatures (
$700\text {--}800\ \text {km}\,\text {s}^{-1}$), and they did not explain the origin of the high coronal temperatures (![]() ${\sim }10^6\ \text {K}$) upon which the models were based.
${\sim }10^6\ \text {K}$) upon which the models were based.
These shortcomings led a number of authors to conjecture that the solar wind is powered to a large extent by an energy flux carried by waves. Several observations support this idea, including in situ measurements of large-amplitude, outward-propagating Alfvén waves (AWs) in the interplanetary medium (e.g. Belcher & Davis Reference Belcher and Davis1971; Tu & Marsch Reference Tu and Marsch1995; Bruno & Carbone Reference Bruno and Carbone2013) and remote observations of AW-like motions in the low corona that carry an energy flux sufficient to power the solar wind (De Pontieu et al. Reference De Pontieu, McIntosh, Carlsson, Hansteen, Tarbell, Schrijver, Title, Shine, Tsuneta and Katsukawa2007).
These observations have stimulated numerous theoretical investigations of how AWs might heat and accelerate the solar wind (see, e.g., Hansteen & Velli Reference Hansteen and Velli2012, and references therein). In many of these models, a substantial fraction of the Sun's AW energy flux is transferred to solar-wind particles by some form of dissipation. Because photospheric motions primarily launch large-wavelength AWs, and because large-wavelength AWs are virtually dissipationless, the AWs are unable to transfer their energy to the plasma near the Sun unless they become turbulent. Turbulence dramatically enhances the rate of AW dissipation because it causes AW energy to cascade from large wavelengths to small wavelengths where dissipation is rapid. One of the dominant nonlinearities that gives rise to AW turbulence is the interaction between counter-propagating AWs (Iroshnikov Reference Iroshnikov1963; Kraichnan Reference Kraichnan1965). Because the Sun launches only outward-propagating waves, solar-wind models that invoke this nonlinearity require some source of inward-propagating AWs. One such source is AW reflection arising from the radial variation in the Alfvén speed (Heinemann & Olbert Reference Heinemann and Olbert1980; Velli Reference Velli1993; Hollweg & Isenberg Reference Hollweg and Isenberg2007). Direct numerical simulations of reflection-driven AW turbulence (RDAWT) in a fast-solar-wind stream emanating from a coronal hole (Perez & Chandran Reference Perez and Chandran2013; van Ballegooijen & Asgari-Targhi Reference van Ballegooijen and Asgari-Targhi2016, Reference van Ballegooijen and Asgari-Targhi2017; Chandran & Perez Reference Chandran and Perez2019) have shown that AW turbulence initiated by wave reflections can drive a vigorous turbulent cascade. The turbulent dissipation rates in the simulations of Perez & Chandran (Reference Perez and Chandran2013) and Chandran & Perez (Reference Chandran and Perez2019) are consistent with the turbulent heating rates in solar-wind models that rely on RDAWT, which have proven quite successful at explaining solar-wind observations (Cranmer, van Ballegooijen & Edgar Reference Cranmer, van Ballegooijen and Edgar2007; Verdini et al. Reference Verdini, Velli, Matthaeus, Oughton and Dmitruk2010; Chandran et al. Reference Chandran, Dennis, Quataert and Bale2011; van der Holst et al. Reference van der Holst, Sokolov, Meng, Jin, Manchester IV, Tóth and Gombosi2014; Usmanov, Goldstein & Matthaeus Reference Usmanov, Goldstein and Matthaeus2014). (We note that there are a number of alternative approaches to incorporating AWs into solar-wind models; see, e.g., Suzuki (Reference Suzuki2006); Suzuki & Inutsuka (Reference Suzuki and Inutsuka2006), Ofman (Reference Ofman2010) and Shoda et al. (Reference Shoda, Suzuki, Asgari-Targhi and Yokoyama2019).)
In addition to solar-wind heating via the cascade and dissipation of AW energy, AWs energize the solar wind through the work done by the AW pressure force, which directly accelerates plasma away from the Sun (e.g. Hollweg Reference Hollweg1973; Wang Reference Wang1993). The relative importance of AW heating and AW work, however, is not well understood. Our goal in this paper is to use direct numerical simulations of RDAWT to determine the fraction of the AW power that is transferred to the solar wind via turbulent dissipation between the coronal base and radius ![]() $r$, denoted by
$r$, denoted by ![]() $\chi _{H}(r)$, and the fraction that is transferred via work, denoted by
$\chi _{H}(r)$, and the fraction that is transferred via work, denoted by ![]() $\chi _{W}(r)$.Footnote 1
$\chi _{W}(r)$.Footnote 1
In § 2, we present the mathematical framework that we use to address this problem and derive mathematical expressions for ![]() $\chi _{H}(r)$ and
$\chi _{H}(r)$ and ![]() $\chi _{W}(r)$. In § 3 we compute
$\chi _{W}(r)$. In § 3 we compute ![]() $\chi _{H}(r)$ and
$\chi _{H}(r)$ and ![]() $\chi _{W}(r)$ in high-resolution numerical simulations of RDAWT with fixed, observationally constrained, model radial profiles for the plasma density, solar-wind outflow velocity, and background magnetic-field strength. We compare our numerical results with the values of
$\chi _{W}(r)$ in high-resolution numerical simulations of RDAWT with fixed, observationally constrained, model radial profiles for the plasma density, solar-wind outflow velocity, and background magnetic-field strength. We compare our numerical results with the values of ![]() $\chi _{H}(r)$ and
$\chi _{H}(r)$ and ![]() $\chi _{W}(r)$ that result from a previously published analytic model of RDAWT (Chandran & Hollweg Reference Chandran and Hollweg2009). We also investigate the radial evolution of the average proton magnetic moment
$\chi _{W}(r)$ that result from a previously published analytic model of RDAWT (Chandran & Hollweg Reference Chandran and Hollweg2009). We also investigate the radial evolution of the average proton magnetic moment ![]() $k_{B} T_{\perp p}(r)/B(r)$ when RDAWT is the dominant proton heating mechanism, where
$k_{B} T_{\perp p}(r)/B(r)$ when RDAWT is the dominant proton heating mechanism, where ![]() $T_{\perp p}$ is the perpendicular proton temperature,
$T_{\perp p}$ is the perpendicular proton temperature, ![]() $k_{B}$ is the Boltzmann constant, and
$k_{B}$ is the Boltzmann constant, and ![]() $B$ is the magnetic-field strength.
$B$ is the magnetic-field strength.
2. Energization of the solar wind by AW turbulence
We consider turbulent fluctuations within a narrow magnetic flux tube of cross-sectional area ![]() $a(r) \ll r^2$, where
$a(r) \ll r^2$, where ![]() $r$ is heliocentric distance. We neglect solar rotation and take this flux tube to be centred on a radial magnetic-field line. We take the density
$r$ is heliocentric distance. We neglect solar rotation and take this flux tube to be centred on a radial magnetic-field line. We take the density ![]() $\rho$, solar-wind outflow velocity
$\rho$, solar-wind outflow velocity ![]() $\boldsymbol {U}$, and background magnetic field
$\boldsymbol {U}$, and background magnetic field ![]() $\boldsymbol {B}_0$ to be fixed functions of
$\boldsymbol {B}_0$ to be fixed functions of ![]() $r$,
$r$,
where ![]() $\boldsymbol {\hat {b}}\equiv \boldsymbol {B}_0/B_0$. Magnetic-flux conservation implies that
$\boldsymbol {\hat {b}}\equiv \boldsymbol {B}_0/B_0$. Magnetic-flux conservation implies that
where ![]() $a_\odot$ and
$a_\odot$ and ![]() $B_\odot$ are the values of
$B_\odot$ are the values of ![]() $a(r)$ and
$a(r)$ and ![]() $B(r)$ at the coronal base, located at
$B(r)$ at the coronal base, located at ![]() $r\simeq R_{\odot }$, where
$r\simeq R_{\odot }$, where ![]() $R_\odot$ is the solar radius. We allow for super-radial expansion of the magnetic field, but assume that
$R_\odot$ is the solar radius. We allow for super-radial expansion of the magnetic field, but assume that ![]() $a/r^2$ is small enough that
$a/r^2$ is small enough that ![]() $\boldsymbol {\hat {b}}$ is nearly radial and
$\boldsymbol {\hat {b}}$ is nearly radial and ![]() $r-R_\odot$ is approximately equal to the distance from the coronal base measured along the magnetic field. We also assume that the fluctuations in the velocity and magnetic field, denoted by
$r-R_\odot$ is approximately equal to the distance from the coronal base measured along the magnetic field. We also assume that the fluctuations in the velocity and magnetic field, denoted by ![]() $\delta \boldsymbol {v}$ and
$\delta \boldsymbol {v}$ and ![]() $\delta \boldsymbol {B}$, are orthogonal to
$\delta \boldsymbol {B}$, are orthogonal to ![]() $\boldsymbol {B}_0$, that
$\boldsymbol {B}_0$, that ![]() $\delta \boldsymbol {v}$ is divergence-free and that density fluctuations are negligibly small.
$\delta \boldsymbol {v}$ is divergence-free and that density fluctuations are negligibly small.
Given these simplifying assumptions, the fluctuations satisfy the equations (see, e.g., Cranmer & van Ballegooijen Reference Cranmer and van Ballegooijen2005; Verdini & Velli Reference Verdini and Velli2007; Chandran & Hollweg Reference Chandran and Hollweg2009)
where ![]() $\boldsymbol {z}^\pm =\delta \boldsymbol {v}\mp \delta \boldsymbol {b}$ are the Elsasser variables,
$\boldsymbol {z}^\pm =\delta \boldsymbol {v}\mp \delta \boldsymbol {b}$ are the Elsasser variables, ![]() $\delta \boldsymbol {v}$ is the fluctuating velocity,
$\delta \boldsymbol {v}$ is the fluctuating velocity, ![]() $\delta \boldsymbol {b}=\delta \boldsymbol {B}/\sqrt {4{\rm \pi} \rho }$ is the fluctuating Alfvén velocity,
$\delta \boldsymbol {b}=\delta \boldsymbol {B}/\sqrt {4{\rm \pi} \rho }$ is the fluctuating Alfvén velocity, ![]() $v_{A} = B_0 /\sqrt {4{\rm \pi} \rho }$ is the Alfvén speed,
$v_{A} = B_0 /\sqrt {4{\rm \pi} \rho }$ is the Alfvén speed, ![]() $P=p+B^2/8{\rm \pi}$ is the combined plasma and magnetic pressure,
$P=p+B^2/8{\rm \pi}$ is the combined plasma and magnetic pressure, ![]() $\boldsymbol {D}^\pm$ is a dissipation term that accounts for viscosity and resistivity (or possibly hyper-viscosity and hyper-resistivity in some numerical models), and
$\boldsymbol {D}^\pm$ is a dissipation term that accounts for viscosity and resistivity (or possibly hyper-viscosity and hyper-resistivity in some numerical models), and
are characteristic length scales of ![]() $\rho$,
$\rho$, ![]() $B_0$ and
$B_0$ and ![]() $v_{A}$ along the magnetic field, respectively. Our definition of Elsasser variables with the ‘
$v_{A}$ along the magnetic field, respectively. Our definition of Elsasser variables with the ‘![]() $\mp$’ sign convention implies that
$\mp$’ sign convention implies that ![]() $\boldsymbol {z}^+$ (
$\boldsymbol {z}^+$ (![]() $\boldsymbol {z}^-$) represents AW fluctuations propagating parallel (anti-parallel) to
$\boldsymbol {z}^-$) represents AW fluctuations propagating parallel (anti-parallel) to ![]() $\boldsymbol {B}_0$ in the local plasma frame. For concreteness, we take
$\boldsymbol {B}_0$ in the local plasma frame. For concreteness, we take ![]() $\boldsymbol {B}_0$ to point radially outward from the Sun so that
$\boldsymbol {B}_0$ to point radially outward from the Sun so that ![]() $\boldsymbol {z}^+$ (
$\boldsymbol {z}^+$ (![]() $\boldsymbol {z}^-$) represents AW fluctuations that propagate anti-Sunward (Sunward) in the plasma frame. Equations (2.3) can be also seen as an inhomogeneous version of the reduced magnetohydrodynamics (RMHD) model (Kadomtsev & Pogutse Reference Kadomtsev and Pogutse1974; Strauss Reference Strauss1976) with an important new piece of physics, namely the linear coupling between
$\boldsymbol {z}^-$) represents AW fluctuations that propagate anti-Sunward (Sunward) in the plasma frame. Equations (2.3) can be also seen as an inhomogeneous version of the reduced magnetohydrodynamics (RMHD) model (Kadomtsev & Pogutse Reference Kadomtsev and Pogutse1974; Strauss Reference Strauss1976) with an important new piece of physics, namely the linear coupling between ![]() $\boldsymbol {z}^+$ and
$\boldsymbol {z}^+$ and ![]() $\boldsymbol {z}^-$ fluctuations that is responsible for the non-WKBFootnote 2 reflection of AWs resulting from the spatial variation of
$\boldsymbol {z}^-$ fluctuations that is responsible for the non-WKBFootnote 2 reflection of AWs resulting from the spatial variation of ![]() $v_{A}$.
$v_{A}$.
2.1. Solar wind energization: how the AW power decreases with  $r$
$r$
The background flow and turbulent fluctuations satisfy a total-energy conservation relation, which in steady state takes the form (Chandran et al. Reference Chandran, Perez, Verscharen, Klein and Mallet2015)
where
is the enthalpy flux of the background plasma, ![]() $G$ is the universal gravitational constant,
$G$ is the universal gravitational constant, ![]() $M_{\odot }$ is the mass of the Sun,
$M_{\odot }$ is the mass of the Sun, ![]() $\gamma$ is the ratio of specific heats,
$\gamma$ is the ratio of specific heats, ![]() $q_r$ is the radial component of the heat flux,
$q_r$ is the radial component of the heat flux,
is the enthalpy flux of the fluctuations,
is the energy flux of the Elsasser field ![]() $\boldsymbol {z}^\pm$,
$\boldsymbol {z}^\pm$,
is the average energy density of Elsasser field ![]() $\boldsymbol {z}^\pm$,
$\boldsymbol {z}^\pm$, ![]() $\left \langle \cdots \right \rangle$ denotes a statistical ensemble average,Footnote 3 and rms denotes the root-mean-square (r.m.s.) value,
$\left \langle \cdots \right \rangle$ denotes a statistical ensemble average,Footnote 3 and rms denotes the root-mean-square (r.m.s.) value,
is the magnetic pressure of the fluctuations and
is the average residual energy density.
Upon taking the dot product of (2.3) with ![]() $\rho \boldsymbol {z}^\pm /2$, performing an ensemble average, and summing the
$\rho \boldsymbol {z}^\pm /2$, performing an ensemble average, and summing the ![]() $+$ and
$+$ and ![]() $-$ versions of the equation, we obtain a separate equation describing the evolution of the fluctuation energy in steady state,
$-$ versions of the equation, we obtain a separate equation describing the evolution of the fluctuation energy in steady state,
where
is the average turbulent heating rate, and ![]() $\sigma =\boldsymbol {\nabla }\boldsymbol {\cdot }\boldsymbol {\hat b}=1/H_B$. When
$\sigma =\boldsymbol {\nabla }\boldsymbol {\cdot }\boldsymbol {\hat b}=1/H_B$. When ![]() ${\mathcal {E}}_{R} \rightarrow 0$,
${\mathcal {E}}_{R} \rightarrow 0$, ![]() ${\mathcal {E}}^-/{\mathcal {E}}^+ \rightarrow 0$ and
${\mathcal {E}}^-/{\mathcal {E}}^+ \rightarrow 0$ and ![]() $Q\rightarrow 0$, equation (2.12) reduces to equation (42) of Dewar (Reference Dewar1970), which is equivalent to the statement that the action of outward-propagating AWs is conserved. Combining (2.7) and (2.12), we obtain the relation
$Q\rightarrow 0$, equation (2.12) reduces to equation (42) of Dewar (Reference Dewar1970), which is equivalent to the statement that the action of outward-propagating AWs is conserved. Combining (2.7) and (2.12), we obtain the relation
where
is the AW power. For the solar wind case, in which ![]() ${\mathcal {E}}^+ > {\mathcal {E}}^-$ and
${\mathcal {E}}^+ > {\mathcal {E}}^-$ and ![]() $P_\textrm {AW} > 0$, equation (2.14) describes how the AW power decreases with increasing
$P_\textrm {AW} > 0$, equation (2.14) describes how the AW power decreases with increasing ![]() $r$. Equation (2.5) implies that
$r$. Equation (2.5) implies that ![]() $P_\textrm {AW}(r) + P_\textrm {flow}(r)$ is independent of
$P_\textrm {AW}(r) + P_\textrm {flow}(r)$ is independent of ![]() $r$, where
$r$, where ![]() $P_\textrm {flow} = a(r) F_\textrm {flow}(r)$ is the power carried by the outflowing background plasma. Thus, as
$P_\textrm {flow} = a(r) F_\textrm {flow}(r)$ is the power carried by the outflowing background plasma. Thus, as ![]() $P_\textrm {AW}$ decreases,
$P_\textrm {AW}$ decreases, ![]() $P_\textrm {flow}$ increases and energy is transferred from the AW fluctuations to the background without loss.
$P_\textrm {flow}$ increases and energy is transferred from the AW fluctuations to the background without loss.
By multiplying (2.14) by ![]() $a(r)$ and integrating from the coronal base at
$a(r)$ and integrating from the coronal base at ![]() $r=r_{b}$ out to radius
$r=r_{b}$ out to radius ![]() $r$, we obtain
$r$, we obtain
where the ‘![]() $b$’ subscript indicates that the subscripted quantity (
$b$’ subscript indicates that the subscripted quantity (![]() $P_\textrm {AW}$ in this case) is evaluated at
$P_\textrm {AW}$ in this case) is evaluated at ![]() $r=r_{b}$. The first term inside the first integral of (2.16) is the negative of the radial component of the pressure force on a plasma parcel of thickness
$r=r_{b}$. The first term inside the first integral of (2.16) is the negative of the radial component of the pressure force on a plasma parcel of thickness ![]() $\textrm {d}r$,
$\textrm {d}r$, ![]() $-a(\text {d} p_{w}/ \text {d} r)\,\textrm {d}r$, multiplied by the radial velocity
$-a(\text {d} p_{w}/ \text {d} r)\,\textrm {d}r$, multiplied by the radial velocity ![]() $U$, which has the familiar force-times-velocity form of mechanical power and represents the rate at which
$U$, which has the familiar force-times-velocity form of mechanical power and represents the rate at which ![]() $P_\textrm {AW}$ decreases with increasing radius due to the work done by AWs on the flow. When residual energy
$P_\textrm {AW}$ decreases with increasing radius due to the work done by AWs on the flow. When residual energy ![]() $\mathcal {E}_{R}$ is negative, which has been shown to result from the nonlinear interaction of counter-propagating AWs (Müller & Grappin Reference Müller and Grappin2005; Boldyrev et al. Reference Boldyrev, Perez, Borovsky and Podesta2011; Wang, Boldyrev & Perez Reference Wang, Boldyrev and Perez2011), the second term in the first integral results in a small reduction of the net work done by the AW pressure. However, positive residual energy is possible in RDAWT when linear terms responsible for non-WKB reflection dominate nonlinear terms and when
$\mathcal {E}_{R}$ is negative, which has been shown to result from the nonlinear interaction of counter-propagating AWs (Müller & Grappin Reference Müller and Grappin2005; Boldyrev et al. Reference Boldyrev, Perez, Borovsky and Podesta2011; Wang, Boldyrev & Perez Reference Wang, Boldyrev and Perez2011), the second term in the first integral results in a small reduction of the net work done by the AW pressure. However, positive residual energy is possible in RDAWT when linear terms responsible for non-WKB reflection dominate nonlinear terms and when ![]() $\text {d} v_{A}/\text {d} r > 0$, in which case the residual energy will be responsible for a slight increase in the net work done by the AW pressure. The second integral in (2.16) represents the rate of decrease in
$\text {d} v_{A}/\text {d} r > 0$, in which case the residual energy will be responsible for a slight increase in the net work done by the AW pressure. The second integral in (2.16) represents the rate of decrease in ![]() $P_\textrm {AW}$ due to dissipation and turbulent heating. We rewrite (2.16) as
$P_\textrm {AW}$ due to dissipation and turbulent heating. We rewrite (2.16) as
where
are the rates at which energy is transferred from the fluctuations to the background flow in the radial interval ![]() $(r_{b}, r)$ via heat and work, respectively. We then divide (2.17) by
$(r_{b}, r)$ via heat and work, respectively. We then divide (2.17) by ![]() $-P_\textrm {AWb}$ and rearrange terms to obtain
$-P_\textrm {AWb}$ and rearrange terms to obtain
where
The first term on the left-hand side of (2.20) is the fraction of the coronal-base AW power ![]() $P_\textrm {AWb}$ that survives to radius
$P_\textrm {AWb}$ that survives to radius ![]() $r$. The second term
$r$. The second term ![]() $\chi _{H}(r)$ is the fraction of
$\chi _{H}(r)$ is the fraction of ![]() $P_\textrm {AWb}$ that is transferred to solar-wind particles via dissipation and heating between
$P_\textrm {AWb}$ that is transferred to solar-wind particles via dissipation and heating between ![]() $r_{b}$ and
$r_{b}$ and ![]() $r$. The third term
$r$. The third term ![]() $\chi _{W}$ is the fraction of
$\chi _{W}$ is the fraction of ![]() $P_\textrm {AWb}$ that is transferred to solar-wind particles via work in the radial interval
$P_\textrm {AWb}$ that is transferred to solar-wind particles via work in the radial interval ![]() $(r_{b}, r)$.
$(r_{b}, r)$.
3. Heat and work fractions of AW power transferred by RDAWT
In this section, we compute the rates at which AW fluctuation energy is transferred to the background solar wind via heating and work in direct numerical simulations of RDAWT. We also compute these same rates using an approximate analytic model of RDAWT. The numerical simulations were carried out using the pseudo-spectral Chebyshev–Fourier REFLECT code (Perez & Chandran Reference Perez and Chandran2013), which solves (2.3) in the narrow-fluxtube geometry described in the previous section.
3.1. Numerical simulations
We consider the three simulations labelled Run 1, Run 2 and Run 3 in the work of Chandran & Perez (Reference Chandran and Perez2019), in which
where ![]() $n$ is the proton number density,
$n$ is the proton number density, ![]() $m_{ p}$ is the proton mass,
$m_{ p}$ is the proton mass, ![]() $x = r/R_\odot$,
$x = r/R_\odot$, ![]() $f_\textrm {max}$ is the super-radial expansion factor (Kopp & Holzer Reference Kopp and Holzer1976), which we set equal to 9,
$f_\textrm {max}$ is the super-radial expansion factor (Kopp & Holzer Reference Kopp and Holzer1976), which we set equal to 9, ![]() $B_\textrm {G}$ is
$B_\textrm {G}$ is ![]() $B_0(r)$ in Gauss and
$B_0(r)$ in Gauss and ![]() $\tilde {n}$ is
$\tilde {n}$ is ![]() $n(r)$ in units of
$n(r)$ in units of ![]() $\text {cm}^{-3}$. In all three runs, the simulation domain consists of a narrow magnetic flux tube with a square cross section of area
$\text {cm}^{-3}$. In all three runs, the simulation domain consists of a narrow magnetic flux tube with a square cross section of area ![]() $[L_\perp (r)]^2$ extending from the photosphere (
$[L_\perp (r)]^2$ extending from the photosphere (![]() $r=R_\odot$) out to approximately
$r=R_\odot$) out to approximately ![]() $r=21 R_\odot$. The Alfvén critical point in these simulations, defined as the heliocentric radius at which the local Alfvén speed equals the solar wind speed, is located at
$r=21 R_\odot$. The Alfvén critical point in these simulations, defined as the heliocentric radius at which the local Alfvén speed equals the solar wind speed, is located at ![]() $r=r_{A}\simeq 11.1R_\odot$ (for a list of relevant heliocentric radii see table 2). Equation (2.2) implies that
$r=r_{A}\simeq 11.1R_\odot$ (for a list of relevant heliocentric radii see table 2). Equation (2.2) implies that
 \begin{equation} L_\perp(r) =L_{{\perp},b}\sqrt{\frac{a(r)}{a_\odot}}=L_{{\perp},b} \sqrt{\frac{B_\odot}{B(r)}}, \end{equation}
\begin{equation} L_\perp(r) =L_{{\perp},b}\sqrt{\frac{a(r)}{a_\odot}}=L_{{\perp},b} \sqrt{\frac{B_\odot}{B(r)}}, \end{equation}
where ![]() $L_{\perp ,b}$ is the width of the simulation domain at the coronal base.
$L_{\perp ,b}$ is the width of the simulation domain at the coronal base.
AWs are injected into the solar corona by imposing a broad spectrum of ![]() $z^+$ fluctuations at the coronal base, located at
$z^+$ fluctuations at the coronal base, located at ![]() $r=1.0026R_\odot$ in our simulations (approximately 1800 km above the photosphere), which then propagate outwards and generate reflected (inward-propagating) waves that drive the turbulent cascade. A strong-turbulence spectrum at the coronal base is achieved by adding a model chromosphere just below the coronal base, with a sharp transition region modelled as a discontinuity of the background profiles. Although the model chromosphere ignores important effects, such as compressibility, it allows us to generate a strong turbulence spectrum of fluctuations driven by reflections from strong inhomogeneities in the chromosphere and the sharp transition region.
$r=1.0026R_\odot$ in our simulations (approximately 1800 km above the photosphere), which then propagate outwards and generate reflected (inward-propagating) waves that drive the turbulent cascade. A strong-turbulence spectrum at the coronal base is achieved by adding a model chromosphere just below the coronal base, with a sharp transition region modelled as a discontinuity of the background profiles. Although the model chromosphere ignores important effects, such as compressibility, it allows us to generate a strong turbulence spectrum of fluctuations driven by reflections from strong inhomogeneities in the chromosphere and the sharp transition region.
The three simulations, which are described in greater detail in Chandran & Perez (Reference Chandran and Perez2019) and a subsequent publication, differ only in the properties of the photospheric velocity field imposed at the inner boundary, namely, the r.m.s. amplitudes of the velocity fluctuations, the correlation lengths and the correlation times. These parameters, listed in table 1, are chosen to investigate how the turbulence properties at each ![]() $r$ depend on the properties of the fluctuations at the coronal base within observational constraints. For instance, the width of the simulation domain at the coronal base,
$r$ depend on the properties of the fluctuations at the coronal base within observational constraints. For instance, the width of the simulation domain at the coronal base, ![]() $L_{\perp ,b}$, is chosen to allow for characteristic correlation lengths of AWs launched at the base to be consistent with observational estimates between
$L_{\perp ,b}$, is chosen to allow for characteristic correlation lengths of AWs launched at the base to be consistent with observational estimates between ![]() $10^3\ \textrm {km}$ to
$10^3\ \textrm {km}$ to ![]() $10^4\ \textrm {km}$ (Dmitruk et al. Reference Dmitruk, Matthaeus, Milano, Oughton, Zank and Mullan2002; Cranmer et al. Reference Cranmer, van Ballegooijen and Edgar2007; Verdini & Velli Reference Verdini and Velli2007; Hollweg, Cranmer & Chandran Reference Hollweg, Cranmer and Chandran2010; Verdini et al. Reference Verdini, Grappin, Pinto and Velli2012; van Ballegooijen & Asgari-Targhi Reference van Ballegooijen and Asgari-Targhi2016, Reference van Ballegooijen and Asgari-Targhi2017). Similarly, photospheric velocity driving with amplitude
$10^4\ \textrm {km}$ (Dmitruk et al. Reference Dmitruk, Matthaeus, Milano, Oughton, Zank and Mullan2002; Cranmer et al. Reference Cranmer, van Ballegooijen and Edgar2007; Verdini & Velli Reference Verdini and Velli2007; Hollweg, Cranmer & Chandran Reference Hollweg, Cranmer and Chandran2010; Verdini et al. Reference Verdini, Grappin, Pinto and Velli2012; van Ballegooijen & Asgari-Targhi Reference van Ballegooijen and Asgari-Targhi2016, Reference van Ballegooijen and Asgari-Targhi2017). Similarly, photospheric velocity driving with amplitude ![]() $\delta v_\textrm {rms}\simeq 1.3\ \textrm {km}\,\textrm {s}^{-1}$ and characteristic times between 3 and 10 min leads to
$\delta v_\textrm {rms}\simeq 1.3\ \textrm {km}\,\textrm {s}^{-1}$ and characteristic times between 3 and 10 min leads to ![]() $\delta v_{\textrm {rms}, b}$ values between
$\delta v_{\textrm {rms}, b}$ values between ![]() $20$ and
$20$ and ![]() $30\ \textrm {km}\,\textrm {s}^{-1}$ with correlation times between
$30\ \textrm {km}\,\textrm {s}^{-1}$ with correlation times between ![]() $0.3$ and
$0.3$ and ![]() $1.6$ min.
$1.6$ min.
Table 1. Relevant simulation parameters. At the photosphere: ![]() $\tau ^+_{c,p}$ is the correlation time of velocity fluctuations imposed at
$\tau ^+_{c,p}$ is the correlation time of velocity fluctuations imposed at ![]() $r=R_\odot$. At the coronal base:
$r=R_\odot$. At the coronal base: ![]() $\tau ^+_{c,p}$ is the correlation time of outward-propagating AWs (
$\tau ^+_{c,p}$ is the correlation time of outward-propagating AWs (![]() $z^+$),
$z^+$), ![]() $L_{\perp ,b}$ is the perpendicular box length,
$L_{\perp ,b}$ is the perpendicular box length, ![]() $z^+_{\textrm {rms}}$ is the r.m.s. amplitude of AWs injected at the base, and
$z^+_{\textrm {rms}}$ is the r.m.s. amplitude of AWs injected at the base, and ![]() $v_\textrm {rms,b}$ is the bulk velocity r.m.s.
$v_\textrm {rms,b}$ is the bulk velocity r.m.s.

3.2. Analytic model of RDAWT
Chandran & Hollweg (Reference Chandran and Hollweg2009) (hereafter CH09) developed an analytic model of RDAWT based on (2.3) but with the additional assumption that
which implies that
Given (3.6), CH09 estimated the turbulent heating rate to be
where ![]() $\lambda _\perp$ is the correlation length of the turbulence measured perpendicular to
$\lambda _\perp$ is the correlation length of the turbulence measured perpendicular to ![]() $\boldsymbol {B}_0$. Following Dmitruk et al. (Reference Dmitruk, Matthaeus, Milano, Oughton, Zank and Mullan2002), CH09 estimated
$\boldsymbol {B}_0$. Following Dmitruk et al. (Reference Dmitruk, Matthaeus, Milano, Oughton, Zank and Mullan2002), CH09 estimated ![]() $z^-_\textrm {rms}$ by balancing the rate at which
$z^-_\textrm {rms}$ by balancing the rate at which ![]() $\boldsymbol {z}^-$ is produced by non-WKB reflection against the rate at which
$\boldsymbol {z}^-$ is produced by non-WKB reflection against the rate at which ![]() $\boldsymbol {z}^-$ cascades to small scales and dissipates in the small-
$\boldsymbol {z}^-$ cascades to small scales and dissipates in the small-![]() $\lambda _\perp$ limit, obtaining
$\lambda _\perp$ limit, obtaining
which is independent of ![]() $z^+_\textrm {rms}$, because the source and sink terms for
$z^+_\textrm {rms}$, because the source and sink terms for ![]() $\boldsymbol {z}^-$ are both proportional to
$\boldsymbol {z}^-$ are both proportional to ![]() $z^+_\textrm {rms}$. CH09 then used (3.6) and (3.9) to solve (2.14), obtaining
$z^+_\textrm {rms}$. CH09 then used (3.6) and (3.9) to solve (2.14), obtaining
 \begin{equation} [z^+_\textrm{rms}(r)]^2 =(z^+_{\textrm{rms},b})^2 \frac{\eta^{1/2}}{\eta_{b}^{1/2}} \left(\frac{1+\eta_{b}^{1/2}}{1+\eta^{1/2}}\right)^2 h(r), \end{equation}
\begin{equation} [z^+_\textrm{rms}(r)]^2 =(z^+_{\textrm{rms},b})^2 \frac{\eta^{1/2}}{\eta_{b}^{1/2}} \left(\frac{1+\eta_{b}^{1/2}}{1+\eta^{1/2}}\right)^2 h(r), \end{equation}where
 \begin{gather} h(r)=\left\{ \begin{array}{@{}cc} v_\textrm{Ab}/v_{A}(r), & \textrm{if}\ r_{b} < r< r_{m},\\ v_\textrm{Ab}v_{A}(r)/v_\textrm{Am}^2, & \textrm{if}\ r > r_{m}, \end{array} \right. \end{gather}
\begin{gather} h(r)=\left\{ \begin{array}{@{}cc} v_\textrm{Ab}/v_{A}(r), & \textrm{if}\ r_{b} < r< r_{m},\\ v_\textrm{Ab}v_{A}(r)/v_\textrm{Am}^2, & \textrm{if}\ r > r_{m}, \end{array} \right. \end{gather}
and ![]() $v_\textrm {Am}$ is the maximum Alfvén speed in the corona, which occurs at
$v_\textrm {Am}$ is the maximum Alfvén speed in the corona, which occurs at ![]() $r=r_{m}$. (CH09 assumed that
$r=r_{m}$. (CH09 assumed that ![]() $v_{A}$ increased monotonically with increasing
$v_{A}$ increased monotonically with increasing ![]() $r$ between
$r$ between ![]() $r_{b}$ and
$r_{b}$ and ![]() $r_{m}$, and then decreased monotonically with increasing
$r_{m}$, and then decreased monotonically with increasing ![]() $r$ at
$r$ at ![]() $r>r_{m}$.) The CH09 model reduces to the model of Dmitruk et al. (Reference Dmitruk, Matthaeus, Milano, Oughton, Zank and Mullan2002) in the limit
$r>r_{m}$.) The CH09 model reduces to the model of Dmitruk et al. (Reference Dmitruk, Matthaeus, Milano, Oughton, Zank and Mullan2002) in the limit ![]() $U\rightarrow 0$.
$U\rightarrow 0$.
Mass and magnetic-flux conservation imply that
This equation and the condition that ![]() $U(r_{A}) = v_{A}(r_{A})$ imply that
$U(r_{A}) = v_{A}(r_{A})$ imply that
The density at the coronal base exceeds the density at the Alfvén critical point by a large factor (![]() $\simeq 10^5$ in the fast-solar-wind model of Chandran et al. Reference Chandran, Dennis, Quataert and Bale2011). Thus,
$\simeq 10^5$ in the fast-solar-wind model of Chandran et al. Reference Chandran, Dennis, Quataert and Bale2011). Thus,
Given (2.15), (3.6), (3.14) and (3.15),
Upon substituting (3.8), (3.9), (3.10) and (3.16) into (2.18) and (2.21a,b), we obtain
Equations (2.15), (3.10) and (3.15) imply that
It then follows from (2.20) and (3.18) that
3.3. The fractions of the AW power that are converted into heat and work
Figure 1 shows the fractions ![]() $\chi _{H},\chi _{W}$ and
$\chi _{H},\chi _{W}$ and ![]() $P_\textrm {AW}/P_\textrm {AWb}$ for Run 1, Run 2 and Run 3, as well as the corresponding fractions calculated from the analytic model described in the previous section, using (3.2), (3.3), (3.4), (3.17), (3.18), (3.19) and the numerical values of relevant parameters listed in table 2. In the simulations, the heating fractions are calculated using (2.9), (2.10), (2.11), (2.13), (2.18) and (2.19). Assuming ergodicity in space and time at each radius, ensemble averages in (2.9), (2.11) and (2.13) are computed using a combined average over time (during the simulation's steady state) and over the cross-sectional area of the fluxtube. More precisely, ensemble averages of any quantity
$P_\textrm {AW}/P_\textrm {AWb}$ for Run 1, Run 2 and Run 3, as well as the corresponding fractions calculated from the analytic model described in the previous section, using (3.2), (3.3), (3.4), (3.17), (3.18), (3.19) and the numerical values of relevant parameters listed in table 2. In the simulations, the heating fractions are calculated using (2.9), (2.10), (2.11), (2.13), (2.18) and (2.19). Assuming ergodicity in space and time at each radius, ensemble averages in (2.9), (2.11) and (2.13) are computed using a combined average over time (during the simulation's steady state) and over the cross-sectional area of the fluxtube. More precisely, ensemble averages of any quantity ![]() $f=f(\boldsymbol {x},t)$ in the simulations are computed as
$f=f(\boldsymbol {x},t)$ in the simulations are computed as
where ![]() $S$ is the cross-sectional surface of the fluxtube at each radius.
$S$ is the cross-sectional surface of the fluxtube at each radius.

Figure 1. Fractions of the Sun's AW power injected at the base ![]() $\chi _{H}(r)$ (solid) and
$\chi _{H}(r)$ (solid) and ![]() $\chi _{W}(r)$ (dashed) that are transferred to solar-wind particles via heating and work, respectively, between the coronal base and heliocentric distance
$\chi _{W}(r)$ (dashed) that are transferred to solar-wind particles via heating and work, respectively, between the coronal base and heliocentric distance ![]() $r$. Here
$r$. Here ![]() $P_\textrm {AW}/P_\textrm {AWb}$ (dashed-dotted) is the fraction of the power that remains at each heliocentric distance
$P_\textrm {AW}/P_\textrm {AWb}$ (dashed-dotted) is the fraction of the power that remains at each heliocentric distance ![]() $r$. These fractions are evaluated for Run 1, Run 2 and Run 3 using the expressions in § 2.1 and for the CH09 analytic model (lower-right panel) using the expressions in § 3.2. All four panels are computed using the
$r$. These fractions are evaluated for Run 1, Run 2 and Run 3 using the expressions in § 2.1 and for the CH09 analytic model (lower-right panel) using the expressions in § 3.2. All four panels are computed using the ![]() $n(r)$,
$n(r)$, ![]() $B_0(r)$ and
$B_0(r)$ and ![]() $U(r)$ profiles in (3.2) through (3.4). The green dotted lines represent the sum of the three fractions, which owing to energy conservation equals one in steady state. Small deviations from one in the numerical simulations are due primarily to averaging over a finite number of realizations rather than a full ensemble representing a true statistical state.
$U(r)$ profiles in (3.2) through (3.4). The green dotted lines represent the sum of the three fractions, which owing to energy conservation equals one in steady state. Small deviations from one in the numerical simulations are due primarily to averaging over a finite number of realizations rather than a full ensemble representing a true statistical state.
Table 2. Glossary of relevant quantities and their numerical values.

The reason that ![]() $\chi _{H}(r_{A})$ is greater than 0.5 in the simulations is that a moderate fraction of the remaining AW energy flux dissipates each time the outward-propagating AWs pass through one Alfvén-speed scale height (Dmitruk et al. Reference Dmitruk, Matthaeus, Milano, Oughton, Zank and Mullan2002; Chandran & Hollweg Reference Chandran and Hollweg2009), and there are a few Alfvén-speed scale heights between
$\chi _{H}(r_{A})$ is greater than 0.5 in the simulations is that a moderate fraction of the remaining AW energy flux dissipates each time the outward-propagating AWs pass through one Alfvén-speed scale height (Dmitruk et al. Reference Dmitruk, Matthaeus, Milano, Oughton, Zank and Mullan2002; Chandran & Hollweg Reference Chandran and Hollweg2009), and there are a few Alfvén-speed scale heights between ![]() $r=r_{b}$ and
$r=r_{b}$ and ![]() $r=r_{A}$. On the other hand, the work fraction
$r=r_{A}$. On the other hand, the work fraction ![]() $\chi _{W}\lesssim 0.3$ is significantly smaller because
$\chi _{W}\lesssim 0.3$ is significantly smaller because ![]() $v_{A} > U$ at
$v_{A} > U$ at ![]() $r < r_{A}$, and thus AWs at
$r < r_{A}$, and thus AWs at ![]() $r < r_{A}$ are in an approximate sense speeding through a quasi-stationary background without doing much work. In contrast, at
$r < r_{A}$ are in an approximate sense speeding through a quasi-stationary background without doing much work. In contrast, at ![]() $r > r_{A}$,
$r > r_{A}$, ![]() $v_{A} < U$ and the AWs can be thought of as being ‘stuck to the plasma’, which enhances the rate at which the fluctuations do work and causes work to become somewhat more efficient than heating. For example,
$v_{A} < U$ and the AWs can be thought of as being ‘stuck to the plasma’, which enhances the rate at which the fluctuations do work and causes work to become somewhat more efficient than heating. For example, ![]() $\chi _{W}(21 R_{\odot }) - \chi _{W}(r_{A})$ equals 0.05, 0.027, 0.062 and 0.017 in Run 1, Run 2, Run 3 and the analytic model, respectively, whereas
$\chi _{W}(21 R_{\odot }) - \chi _{W}(r_{A})$ equals 0.05, 0.027, 0.062 and 0.017 in Run 1, Run 2, Run 3 and the analytic model, respectively, whereas ![]() $\chi _{H}(21 R_{\odot }) - \chi _{H}(r_{A})$ equals 0.04, 0.026, 0.055 and 0.016 in Run 1, Run 2, Run 3 and the analytic model, respectively. Although work is slightly more efficient than heating at transferring energy from AWs to solar-wind particles between
$\chi _{H}(21 R_{\odot }) - \chi _{H}(r_{A})$ equals 0.04, 0.026, 0.055 and 0.016 in Run 1, Run 2, Run 3 and the analytic model, respectively. Although work is slightly more efficient than heating at transferring energy from AWs to solar-wind particles between ![]() $r=r_{A}$ and
$r=r_{A}$ and ![]() $r=21R_{\odot }$, most of the AW energy flux has dissipated by the time the AWs reach
$r=21R_{\odot }$, most of the AW energy flux has dissipated by the time the AWs reach ![]() $r_{A}$, and the amount of AW power that is transferred to particles via work in this region is only a tiny fraction (
$r_{A}$, and the amount of AW power that is transferred to particles via work in this region is only a tiny fraction (![]() $\lesssim 6\,\%$) of
$\lesssim 6\,\%$) of ![]() $P_\textrm {AWb}$.
$P_\textrm {AWb}$.
The different efficiencies of AW energy loss via work inside and outside the Alfvén critical point are in some ways analogous to the different rates at which energetic particles lose energy in the expanding solar wind in the scatter-free and scatter-dominated regimes (Ruffolo Reference Ruffolo1995). When pitch-angle scattering is weak, energetic particles race through the plasma, their energies are approximately conserved, and they do negligible work on the plasma. In contrast, when pitch-angle scattering is strong, energetic particles are ‘stuck to the plasma’, and they lose energy through adiabatic expansion, because the scattering centers that ‘collide’ with the particles are rooted in the plasma and diverge from one another as the plasma expands. As the particles lose energy, they do work on the background flow.
In figure 2(a), we plot the ratio of ![]() $Q$ to
$Q$ to ![]() $|U \,\text {d} p_{W}/\text {d} r - \sigma U {\mathcal {E}}_{R}|$. These two quantities are the rates of heating and work per unit volume, which appear on the right-hand side of (2.16). This figure further illustrates the increasing relative efficiency of work beyond the Alfvén critical point, where the AWs become less mobile with respect to the plasma frame. The sharp feature in
$|U \,\text {d} p_{W}/\text {d} r - \sigma U {\mathcal {E}}_{R}|$. These two quantities are the rates of heating and work per unit volume, which appear on the right-hand side of (2.16). This figure further illustrates the increasing relative efficiency of work beyond the Alfvén critical point, where the AWs become less mobile with respect to the plasma frame. The sharp feature in ![]() $Q/|U \,\text {d} p_{W}/\text {d} r - \sigma U {\mathcal {E}}_{R}|$ at
$Q/|U \,\text {d} p_{W}/\text {d} r - \sigma U {\mathcal {E}}_{R}|$ at ![]() $r=r_{m} = 1.72 R_{\odot }$ in the analytic model (in which
$r=r_{m} = 1.72 R_{\odot }$ in the analytic model (in which ![]() ${\mathcal {E}}_{R}$ is taken to be negligible in comparison with
${\mathcal {E}}_{R}$ is taken to be negligible in comparison with ![]() $p_{W}$) is an artefact of the local nature of the CH09 model, in which
$p_{W}$) is an artefact of the local nature of the CH09 model, in which ![]() $z^-_\textrm {rms}$ is determined at each
$z^-_\textrm {rms}$ is determined at each ![]() $r$ by balancing the local rate of wave reflection against the local rate at which
$r$ by balancing the local rate of wave reflection against the local rate at which ![]() $\boldsymbol {z}^-$ fluctuations cascade and dissipate. This local balance causes
$\boldsymbol {z}^-$ fluctuations cascade and dissipate. This local balance causes ![]() $z^-_\textrm {rms}$ and
$z^-_\textrm {rms}$ and ![]() $Q$ to be proportional to
$Q$ to be proportional to ![]() $|\text {d} v_{A}/\text {d} r|$, which vanishes at
$|\text {d} v_{A}/\text {d} r|$, which vanishes at ![]() $r=r_{m}$. In our numerical simulations,
$r=r_{m}$. In our numerical simulations, ![]() $\boldsymbol {z}^-$ fluctuations propagate some radial distance before dissipating, and
$\boldsymbol {z}^-$ fluctuations propagate some radial distance before dissipating, and ![]() $z^-_\textrm {rms}$ and
$z^-_\textrm {rms}$ and ![]() $Q$ remain non-zero at
$Q$ remain non-zero at ![]() $r=r_{m}$, as seen in the
$r=r_{m}$, as seen in the ![]() $Q$ profiles for numerical simulations shown in figure 2.
$Q$ profiles for numerical simulations shown in figure 2.

Figure 2. (a) The ratio of the heating rate ![]() $Q$ to the rate at which AWs do work on the flow per unit volume,
$Q$ to the rate at which AWs do work on the flow per unit volume, ![]() $|U \,\text {d} p_{w}/\text {d} r-\sigma \mathcal {E}_{R}|$, as a function of heliocentric distance
$|U \,\text {d} p_{w}/\text {d} r-\sigma \mathcal {E}_{R}|$, as a function of heliocentric distance ![]() $r$. Heating is much more efficient than work close to the Sun, but at
$r$. Heating is much more efficient than work close to the Sun, but at ![]() $r>r_{A} = 11.1R_{\odot }$, work becomes slightly more efficient than heating. Right panel: The average proton magnetic moment,
$r>r_{A} = 11.1R_{\odot }$, work becomes slightly more efficient than heating. Right panel: The average proton magnetic moment, ![]() $k_{B} T_{\perp p}/B$, as a function of heliocentric distance
$k_{B} T_{\perp p}/B$, as a function of heliocentric distance ![]() $r$, computed using (3.8), (3.9), (3.10), (3.22), (3.2), (3.3) and (3.4), with
$r$, computed using (3.8), (3.9), (3.10), (3.22), (3.2), (3.3) and (3.4), with ![]() $f_{\perp p} =0.9$,
$f_{\perp p} =0.9$, ![]() $z^+_\textrm {rms,b} = 72\ \text {km}\, \text {s}^{-1}$ and
$z^+_\textrm {rms,b} = 72\ \text {km}\, \text {s}^{-1}$ and ![]() $T_{\perp pb} = 10^6\ \text {K}$.
$T_{\perp pb} = 10^6\ \text {K}$.
3.4. Magnetic-moment production
Beyond the sonic point at ![]() $r=r_{s}$ (
$r=r_{s}$ (![]() $r_{s} \simeq 2 R_{\odot }$ in coronal holes), the solar-wind outflow velocity exceeds the proton thermal speed
$r_{s} \simeq 2 R_{\odot }$ in coronal holes), the solar-wind outflow velocity exceeds the proton thermal speed ![]() $v_\textrm {Tp}$, and the expansion time scale
$v_\textrm {Tp}$, and the expansion time scale ![]() $r/U$ becomes shorter than the minimum time in which heat can conduct over a distance
$r/U$ becomes shorter than the minimum time in which heat can conduct over a distance ![]() $r$, which is approximately
$r$, which is approximately ![]() $r/v_\textrm {Tp}$. Proton thermal conduction can thus be neglected to a reasonable approximation at
$r/v_\textrm {Tp}$. Proton thermal conduction can thus be neglected to a reasonable approximation at ![]() $r>r_{s}$. For simplicity, in this section, we neglect proton thermal conduction at all
$r>r_{s}$. For simplicity, in this section, we neglect proton thermal conduction at all ![]() $r$. We also neglect energy transfer from proton–electron collisions, as well as temperature isotropization from collisions and instabilities. The rate at which the average proton magnetic moment
$r$. We also neglect energy transfer from proton–electron collisions, as well as temperature isotropization from collisions and instabilities. The rate at which the average proton magnetic moment ![]() $k_{B} T_{\perp p}/B$ increases with
$k_{B} T_{\perp p}/B$ increases with ![]() $r$ is then given by Sharma et al. (Reference Sharma, Hammett, Quataert and Stone2006) and Chandran et al. (Reference Chandran, Dennis, Quataert and Bale2011)
$r$ is then given by Sharma et al. (Reference Sharma, Hammett, Quataert and Stone2006) and Chandran et al. (Reference Chandran, Dennis, Quataert and Bale2011)
where ![]() $k_{B}$ is the Boltzmann constant,
$k_{B}$ is the Boltzmann constant, ![]() $T_{\perp p}$ is the perpendicular proton temperature and
$T_{\perp p}$ is the perpendicular proton temperature and ![]() $f_{\perp p}(r)$ is the fraction of the heating rate that goes into perpendicular proton heating at heliocentric distance
$f_{\perp p}(r)$ is the fraction of the heating rate that goes into perpendicular proton heating at heliocentric distance ![]() $r$. We approximate (3.21) by setting
$r$. We approximate (3.21) by setting ![]() $B(r) = B_0(r)$. Upon dividing (3.21) by
$B(r) = B_0(r)$. Upon dividing (3.21) by ![]() $B_0 nU$, integrating and making use of (3.13), we obtain
$B_0 nU$, integrating and making use of (3.13), we obtain
The form of the integrand in (3.22) shows that a given amount of heating produces more magnetic moment in regions of weaker magnetic field.
In figure 2(b), we plot the average magnetic moment ![]() $k_{B} T_{\perp p}/B$ as a function of
$k_{B} T_{\perp p}/B$ as a function of ![]() $r$ using (3.2), (3.3), (3.4), (3.8), (3.9), (3.10) and (3.22), with
$r$ using (3.2), (3.3), (3.4), (3.8), (3.9), (3.10) and (3.22), with ![]() $f_{\perp p} = 0.9$,
$f_{\perp p} = 0.9$, ![]() $z^+_\textrm {rms,b} = 72\ \text {km}\,\text {s}^{-1}$ and
$z^+_\textrm {rms,b} = 72\ \text {km}\,\text {s}^{-1}$ and ![]() $T_{\perp p b} = 10^6\ \text {K}$. Figures 1 and 2 show that, although only a small fraction of
$T_{\perp p b} = 10^6\ \text {K}$. Figures 1 and 2 show that, although only a small fraction of ![]() $P_\textrm {AWb}$ is dissipated at
$P_\textrm {AWb}$ is dissipated at ![]() $r>r_{A}$,
$r>r_{A}$, ![]() $k_{B} T_{\perp p}/B$ rises robustly at
$k_{B} T_{\perp p}/B$ rises robustly at ![]() $r>r_{A}$.
$r>r_{A}$.
4. Conclusion
In this paper, we have used direct numerical simulations of RDAWT to determine ![]() $\chi _{H}(r)$ and
$\chi _{H}(r)$ and ![]() $\chi _{W}(r)$, the fractions of the AW power at the coronal base (
$\chi _{W}(r)$, the fractions of the AW power at the coronal base (![]() $P_\textrm {AWb}$) that are transferred to the solar wind via heating and work between the coronal base (
$P_\textrm {AWb}$) that are transferred to the solar wind via heating and work between the coronal base (![]() $r=r_{b}$) and radius
$r=r_{b}$) and radius ![]() $r$. Our simulations solve for the evolution of transverse, non-compressive fluctuations in a fixed background solar wind whose density, magnetic-field strength and outflow-velocity profiles are chosen to emulate a fast-solar-wind stream emanating from a coronal hole. We have found that heating from the cascade and dissipation of AW fluctuations between
$r$. Our simulations solve for the evolution of transverse, non-compressive fluctuations in a fixed background solar wind whose density, magnetic-field strength and outflow-velocity profiles are chosen to emulate a fast-solar-wind stream emanating from a coronal hole. We have found that heating from the cascade and dissipation of AW fluctuations between ![]() $r_{b}$ and the Alfvén critical point
$r_{b}$ and the Alfvén critical point ![]() $r_{A}$ transfers between 50 % and 70 % of
$r_{A}$ transfers between 50 % and 70 % of ![]() $P_\textrm {AWb}$ to the solar wind, whereas work in this same region transfers between 15 % and 30 % of
$P_\textrm {AWb}$ to the solar wind, whereas work in this same region transfers between 15 % and 30 % of ![]() $P_\textrm {AWb}$ to the solar wind. The variation in these numbers arises from the different photospheric boundary conditions imposed in our different numerical simulations.
$P_\textrm {AWb}$ to the solar wind. The variation in these numbers arises from the different photospheric boundary conditions imposed in our different numerical simulations.
The reason that ![]() $\chi _{H}(r_{A})$ is in the range of 50–70 % is that a moderate fraction of the local AW power dissipates within each Alfvén speed scale height (Dmitruk et al. Reference Dmitruk, Matthaeus, Milano, Oughton, Zank and Mullan2002; Chandran & Hollweg Reference Chandran and Hollweg2009), and there are a few Alfvén speed scale heights between
$\chi _{H}(r_{A})$ is in the range of 50–70 % is that a moderate fraction of the local AW power dissipates within each Alfvén speed scale height (Dmitruk et al. Reference Dmitruk, Matthaeus, Milano, Oughton, Zank and Mullan2002; Chandran & Hollweg Reference Chandran and Hollweg2009), and there are a few Alfvén speed scale heights between ![]() $r_{b}$ and
$r_{b}$ and ![]() $r_{A}$. The reason that
$r_{A}$. The reason that ![]() $\chi _{W}(r_{A})$ is small compared with one is that
$\chi _{W}(r_{A})$ is small compared with one is that ![]() $v_{A} > U$ at
$v_{A} > U$ at ![]() $r < r_{A}$, so AWs in this sub-Alfvénic region are in an approximate sense speeding through a quasi-stationary background without doing much work. Work becomes relatively more efficient at transferring AW energy to the particles at
$r < r_{A}$, so AWs in this sub-Alfvénic region are in an approximate sense speeding through a quasi-stationary background without doing much work. Work becomes relatively more efficient at transferring AW energy to the particles at ![]() $r > r_{A}$, where
$r > r_{A}$, where ![]() $v_{A} < U$ and the AWs are in an approximate sense ‘stuck to the plasma’. However, because most of the Sun's AW power dissipates via heating before the AWs reach
$v_{A} < U$ and the AWs are in an approximate sense ‘stuck to the plasma’. However, because most of the Sun's AW power dissipates via heating before the AWs reach ![]() $r_{A}$, the total rate at which work transfers AW energy to the plasma at
$r_{A}$, the total rate at which work transfers AW energy to the plasma at ![]() $r > r_{A}$ is a small fraction of
$r > r_{A}$ is a small fraction of ![]() $P_\textrm {AWb}$. Although only a small fraction of
$P_\textrm {AWb}$. Although only a small fraction of ![]() $P_\textrm {AWb}$ survives to reach
$P_\textrm {AWb}$ survives to reach ![]() $r_{A}$, the average proton magnetic moment increases robustly at
$r_{A}$, the average proton magnetic moment increases robustly at ![]() $r > r_{A}$ (assuming that a substantial fraction of the turbulent heating rate goes into perpendicular proton heating at these radii), because heating becomes more effective at producing magnetic moment in regions of weaker magnetic field.
$r > r_{A}$ (assuming that a substantial fraction of the turbulent heating rate goes into perpendicular proton heating at these radii), because heating becomes more effective at producing magnetic moment in regions of weaker magnetic field.
The accuracy of our results is limited by our neglect of compressive fluctuations, which enhance the dissipation of AW energy via ‘AW phase mixing’ (Heyvaerts & Priest Reference Heyvaerts and Priest1983). Plasma compressibility further enhances the rate of AW dissipation via parametric decay (Galeev & Oraevskii Reference Galeev and Oraevskii1963; Sagdeev & Galeev Reference Sagdeev and Galeev1969; Cohen & Dewar Reference Cohen and Dewar1974; Goldstein Reference Goldstein1978; Spangler Reference Spangler1986; Hollweg Reference Hollweg1994; Dorfman & Carter Reference Dorfman and Carter2016; Tenerani, Velli & Hellinger Reference Tenerani, Velli and Hellinger2017; Chandran Reference Chandran2018). Three-dimensional compressible MHD simulations of the turbulent solar wind from ![]() $r=r_{b}$ out to
$r=r_{b}$ out to ![]() $r > r_{A}$, such as those carried out by Shoda et al. (Reference Shoda, Suzuki, Asgari-Targhi and Yokoyama2019), could lead to improved estimates of
$r > r_{A}$, such as those carried out by Shoda et al. (Reference Shoda, Suzuki, Asgari-Targhi and Yokoyama2019), could lead to improved estimates of ![]() $\chi _{H}(r)$ and
$\chi _{H}(r)$ and ![]() $\chi _{W}(r)$.
$\chi _{W}(r)$.
Acknowledgements
We thank J. Hollweg, M. Lee, B. Metzger and E. Quataert for valuable discussions. J.C.P. was supported by NSF grant AGS-1752827. B.D.G.C. was supported in part by NASA grants NNX17AI18G and 80NSSC19K0829 and NASA grant NNN06AA01C to the Parker Solar Probe FIELDS Experiment. K.G.K. was supported in part by NASA ECIP grant 80NSSC19K0912 and the Parker Solar Probe SWEAP contract NNN06AA01C. M.M. was supported in part by NASA grant 80NSSC19K1390. An award of computer time was provided by the Innovative and Novel Computational Impact on Theory and Experiment (INCITE) program. During the INCITE award period (from 2012 to 2014), this research used resources of the Argonne Leadership Computing Facility, which is a DOE Office of Science User Facility supported under Contract DE-AC02-06CH11357. This work also used high-performance computing resources of the Texas Advanced Computing Center (TACC) at the University of Texas at Austin, under project TG-ATM100031 of the Extreme Science and Engineering Discovery Environment (XSEDE), which is supported by National Science Foundation grant number ACI-1548562.
Editor Alex Schekochihin thanks the referees for their advice in evaluating this article.
Declaration of interests
The authors report no conflicts of interest.