Article contents
Geometric particle-in-cell methods for the Vlasov–Maxwell equations with spin effects
Published online by Cambridge University Press: 28 May 2021
Abstract
We propose a numerical scheme to solve the semiclassical Vlasov–Maxwell equations for electrons with spin. The electron gas is described by a distribution function $f(t,{\boldsymbol x},{{{\boldsymbol p}}}, {\boldsymbol s})$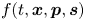 that evolves in an extended 9-dimensional phase space $({\boldsymbol x},{{{\boldsymbol p}}}, {\boldsymbol s})$
that evolves in an extended 9-dimensional phase space $({\boldsymbol x},{{{\boldsymbol p}}}, {\boldsymbol s})$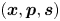 , where $\boldsymbol s$
, where $\boldsymbol s$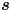 represents the spin vector. Using suitable approximations and symmetries, the extended phase space can be reduced to five dimensions: $(x,{{p_x}}, {\boldsymbol s})$
represents the spin vector. Using suitable approximations and symmetries, the extended phase space can be reduced to five dimensions: $(x,{{p_x}}, {\boldsymbol s})$ . It can be shown that the spin Vlasov–Maxwell equations enjoy a Hamiltonian structure that motivates the use of the recently developed geometric particle-in-cell (PIC) methods. Here, the geometric PIC approach is generalized to the case of electrons with spin. Total energy conservation is very well satisfied, with a relative error below $0.05\,\%$
. It can be shown that the spin Vlasov–Maxwell equations enjoy a Hamiltonian structure that motivates the use of the recently developed geometric particle-in-cell (PIC) methods. Here, the geometric PIC approach is generalized to the case of electrons with spin. Total energy conservation is very well satisfied, with a relative error below $0.05\,\%$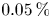 . As a relevant example, we study the stimulated Raman scattering of an electromagnetic wave interacting with an underdense plasma, where the electrons are partially or fully spin polarized. It is shown that the Raman instability is very effective in destroying the electron polarization.
. As a relevant example, we study the stimulated Raman scattering of an electromagnetic wave interacting with an underdense plasma, where the electrons are partially or fully spin polarized. It is shown that the Raman instability is very effective in destroying the electron polarization.
Information
- Type
- Research Article
- Information
- Copyright
- Copyright © The Author(s), 2021. Published by Cambridge University Press
References
REFERENCES
- 7
- Cited by


